题目内容
9. 如图,在△ABC中,AB=AC,∠BAC=120°,AC的垂直平分线EF交AC于F,交BC于E.求证:BE=2CE.
如图,在△ABC中,AB=AC,∠BAC=120°,AC的垂直平分线EF交AC于F,交BC于E.求证:BE=2CE.
分析 利用辅助线,连接AE,求出CE=AE,∠BAE=90°,再根据AB=AC,∠BAC=120°可求出∠B的度数,由直角三角形的性质即可求出BE=2AE=2CE.
解答 证明:如图,连接AE,
∵AB=AC,∠BAC=120°,
∴∠B=∠C=(180°-120°)÷2=30°,
∵AC的垂直平分线EF交AC于点F,交BC于点E,
∴CE=AE(线段垂直平分线上的点到线段两端点的距离相等),
∴∠EAC=∠C=30°(等边对等角),
∴∠BAE=∠BAC-∠EAC=120°-30°=90°,
在Rt△ABE中,∠B=30°,
∴BE=2AE(在直角三角形中,30°角所对的直角边等于斜边的一半),
∴BE=2CE(等量代换).
点评 本题考查的是线段垂直平分线的性质,解决本题的关键是熟记垂直平分线上任意一点,和线段两端点的距离相等.

练习册系列答案
相关题目
19.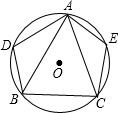 如图所示,△ABC的三个顶点在⊙O上,D是$\widehat{AB}$上的点,E是$\widehat{AC}$上的点,若∠BAC=50°.则∠D+∠E=( )
如图所示,△ABC的三个顶点在⊙O上,D是$\widehat{AB}$上的点,E是$\widehat{AC}$上的点,若∠BAC=50°.则∠D+∠E=( )
 如图所示,△ABC的三个顶点在⊙O上,D是$\widehat{AB}$上的点,E是$\widehat{AC}$上的点,若∠BAC=50°.则∠D+∠E=( )
如图所示,△ABC的三个顶点在⊙O上,D是$\widehat{AB}$上的点,E是$\widehat{AC}$上的点,若∠BAC=50°.则∠D+∠E=( )| A. | 220° | B. | 230° | C. | 240° | D. | 250°° |
18.若方程组$\left\{\begin{array}{l}ax-y=b\\ 3x+by=a\end{array}\right.$的解是$\left\{\begin{array}{l}x=1\\ y=2\end{array}\right.$,则$\frac{a+3b}{a-b}$的值为( )
| A. | $\frac{1}{3}$ | B. | 2 | C. | -1 | D. | 1 |
11.已知点(-2,1)在双曲线y=$\frac{k}{x}$上,则下列各点一定在该双曲线上的是( )
| A. | (1,-2) | B. | (-2,-1) | C. | (2,1) | D. | (1,2) |
 如图,OP平分∠BOA,∠BOA=45°,PC∥OA,PD⊥OA.若PC=2$\sqrt{2}$,求PD的长度.
如图,OP平分∠BOA,∠BOA=45°,PC∥OA,PD⊥OA.若PC=2$\sqrt{2}$,求PD的长度.