题目内容
5.先化简再求值:$\frac{{x}^{2}-2x}{{x}^{2}-4}÷(x-2-\frac{2x-4}{x+2})$,其中x=3$\sqrt{2}$+2.分析 原式括号中两项通分并利用同分母分式的减法法则计算,同时利用除法法则变形,约分得到最简结果,把x的值代入计算即可求出值.
解答 解:原式=$\frac{x(x-2)}{(x+2)(x-2)}$÷$\frac{{x}^{2}-4-2x+4}{x+2}$=$\frac{x}{x+2}$•$\frac{x+2}{x(x-2)}$=$\frac{1}{x-2}$,
当x=3$\sqrt{2}$+2时,原式=$\frac{1}{3\sqrt{2}+2-2}$=$\frac{\sqrt{2}}{6}$.
点评 此题考查了分式的化简求值,熟练掌握运算法则是解本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
13.下列各式结果是0的是( )
| A. | (-3)+(-3) | B. | (-3)-(-3) | C. | (-3)×(-3) | D. | (-3)÷(-3) |
20.实验二中举行了“班班有歌声”活动,比赛聘请了10位老师和10位学生担任评委,其中七(1)班的得分情况如统计图(表)所示
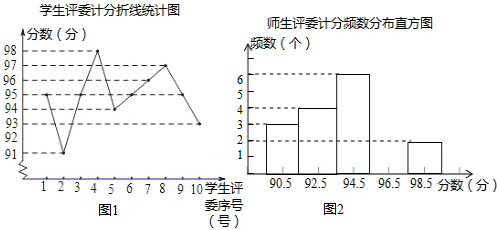
老师评委计分统计表
(1)在频数分布直方图中,自左向右第四组的频数为5
(2)学生评委计分的中位数是95分
(3)计算各班最后得分的规定如下:在评委的计分中各去掉一个最高分、一个最低分,然后计算平均数:分别计算老师、学生评委的平均分:老师、学生评委的平均分各占60%、40%的方法计算各班最后得分,已知七(1)班租后得分为94.4分,求统计表中x的值.

老师评委计分统计表
| 评委序号(号) | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 计分(分) | 94 | 96 | 93 | 91 | x | 91 | 91 | 98 | 96 | 93 |
(2)学生评委计分的中位数是95分
(3)计算各班最后得分的规定如下:在评委的计分中各去掉一个最高分、一个最低分,然后计算平均数:分别计算老师、学生评委的平均分:老师、学生评委的平均分各占60%、40%的方法计算各班最后得分,已知七(1)班租后得分为94.4分,求统计表中x的值.
1.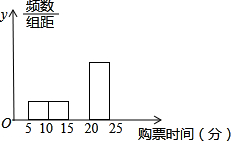 某车站在春运期间为改进服务,随机抽样调查了100名旅客从开始在购票窗口排队到够到车票所用的时间t(以下简称购票用时,单位为分钟).下面是这次调查统计分析得到的频率分布表和频率分布直方图.解答下列问题:
某车站在春运期间为改进服务,随机抽样调查了100名旅客从开始在购票窗口排队到够到车票所用的时间t(以下简称购票用时,单位为分钟).下面是这次调查统计分析得到的频率分布表和频率分布直方图.解答下列问题:
(1)在表中填写确实的数据并补全频率分布直方图;
(2)旅客购票所用的时间平均数可能落在第4组;
(3)若每增加一个购票窗口可以使平均购票用时降低5分钟,要使平均购票用时不超过10分钟,那么请你估计最少需增加几个窗口?
 某车站在春运期间为改进服务,随机抽样调查了100名旅客从开始在购票窗口排队到够到车票所用的时间t(以下简称购票用时,单位为分钟).下面是这次调查统计分析得到的频率分布表和频率分布直方图.解答下列问题:
某车站在春运期间为改进服务,随机抽样调查了100名旅客从开始在购票窗口排队到够到车票所用的时间t(以下简称购票用时,单位为分钟).下面是这次调查统计分析得到的频率分布表和频率分布直方图.解答下列问题:(1)在表中填写确实的数据并补全频率分布直方图;
(2)旅客购票所用的时间平均数可能落在第4组;
(3)若每增加一个购票窗口可以使平均购票用时降低5分钟,要使平均购票用时不超过10分钟,那么请你估计最少需增加几个窗口?
| 分 组 | 频数 | 频率 | |
| 一组 | 0≤t<5 | 0 | 0 |
| 二组 | 5≤t<10 | 10 | 0.10 |
| 三组 | 10≤t<15 | 10 | 0.10 |
| 四组 | 15≤t<20 | 50 | 0.50 |
| 五组 | 20≤t<25 | 30 | 0.30 |
| 合 计 | 100 | 1 |
 如图,在四边形ABCD中,∠B=40°,∠A=140°,∠C=140°,求证:四边形ABCD是平行四边形.
如图,在四边形ABCD中,∠B=40°,∠A=140°,∠C=140°,求证:四边形ABCD是平行四边形.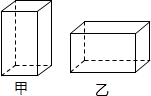 某纸品厂要制作如图所示的甲、乙两种无盖的长方体小盒,该长利用边角料裁出了长方形和正方形两种纸片,其中长方形纸片的宽与正方形纸片的边长相等,现用70张正方形纸片和180张长方形纸片制作这两种小盒(不计算连接部分),则可以制作甲、乙两种小盒各多少个?
某纸品厂要制作如图所示的甲、乙两种无盖的长方体小盒,该长利用边角料裁出了长方形和正方形两种纸片,其中长方形纸片的宽与正方形纸片的边长相等,现用70张正方形纸片和180张长方形纸片制作这两种小盒(不计算连接部分),则可以制作甲、乙两种小盒各多少个?