题目内容
⊙O的直径为10cm，P是⊙O内一点，OP长4cm，过点P的弦长为整数的弦共有 条．
考点：垂径定理,勾股定理
专题：
分析：利用垂径定理档知当过点P的弦垂直直径时最短，直径最长，再结合圆的对称性可得出答案．
解答：
解：
如图，AB是直径，OA=5cm，OP=4cm，过点P作CD⊥AB，交圆于点C，D两点．
由垂径定理知，点P是CD的中点，由勾股定理求得，PC=3cm，CD=6cm，则CD是过点P最短的弦，长为6cm；
AB是过P最长的弦，长为10cm．
由圆的对称性知，过点P的弦的弦长长度为7cm，8cm，9cm的弦分别有2条，过点P的弦的弦长是6cm，10cm的各有1条，则总共有6+2=8条长度为整数的弦．
故答案为：8．
解：如图，AB是直径，OA=5cm，OP=4cm，过点P作CD⊥AB，交圆于点C，D两点．
由垂径定理知，点P是CD的中点，由勾股定理求得，PC=3cm，CD=6cm，则CD是过点P最短的弦，长为6cm；
AB是过P最长的弦，长为10cm．
由圆的对称性知，过点P的弦的弦长长度为7cm，8cm，9cm的弦分别有2条，过点P的弦的弦长是6cm，10cm的各有1条，则总共有6+2=8条长度为整数的弦．
故答案为：8．
点评：本题主要考查垂径定理及圆的对称性质，掌握过圆心的弦是最长的弦是解题的关键．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
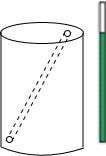如图所示，一个油漆桶高1m，桶内还有剩余油漆，一根木棒长1.5m，小明把木棒从桶盖小口斜插入桶内，一端触到桶底边缘时，另一端恰好与桶盖小口相齐，抽出木棒，量得木棒上浸沾油漆的部分长0.75m，那么桶内油漆面的高度是多少？（油漆桶水平放置）
已知：如图，在△ABC中，AB=2，BC=4，D为BC边上一点，BD=1，求证：△ABC∽△DBA．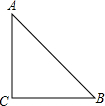
如图，在△ABC中，AC=BC=2cm，∠C=90°，按下列条件建立坐标系，写出顶点的坐标．