题目内容
16. 如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于点D,E是AB的中点,∠ACD=1.5∠DCE,则∠A=22.5°.
如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于点D,E是AB的中点,∠ACD=1.5∠DCE,则∠A=22.5°.
分析 根据已知条件得到AE=CE,根据等腰三角形的性质得到∠A=∠ACE,于是得到∠A=$\frac{1}{3}∠$ACD,即可得到结论.
解答 解:∵∠ACB=90°,E是AB的中点,
∴AE=CE,
∴∠A=∠ACE,
∵∠ACD=1.5∠DCE,
∴∠A=$\frac{1}{3}∠$ACD,
∵CD⊥AB,
∴∠ADC=90°,
∴∠A=90°×$\frac{1}{1+3}$=22.5°,
故答案为:22.5°.
点评 本题考查了直角三角形斜边上的中线等于斜边的一半的性质,等腰三角形的性质,等腰直角三角形的判定与性质,熟记性质并准确识图是解题的关键.

练习册系列答案
相关题目
6.下列图案中,是轴对称图形,但不是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
7.若函数y=-2x-1与函数y=$\frac{k}{x}$的图象相交于点P(-2,m),则下列各点不在函数y=$\frac{k}{x}$的图象上的是( )
| A. | (3,-2) | B. | (1,-6) | C. | (-1,6) | D. | (-1,-6) |
4. 将一把直尺与一块三角板如图所示放置,若∠1=40°,则∠2的度数为( )
将一把直尺与一块三角板如图所示放置,若∠1=40°,则∠2的度数为( )
 将一把直尺与一块三角板如图所示放置,若∠1=40°,则∠2的度数为( )
将一把直尺与一块三角板如图所示放置,若∠1=40°,则∠2的度数为( )| A. | 50° | B. | 110° | C. | 130° | D. | 150° |
11.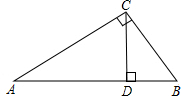 如图,AC⊥BC,CD⊥AB,垂足分别为C、D,下列说法不正确的是( )
如图,AC⊥BC,CD⊥AB,垂足分别为C、D,下列说法不正确的是( )
 如图,AC⊥BC,CD⊥AB,垂足分别为C、D,下列说法不正确的是( )
如图,AC⊥BC,CD⊥AB,垂足分别为C、D,下列说法不正确的是( )| A. | 点A到BC的距离是AC的长度 | B. | 点B到AC的距离是BC的长度 | ||
| C. | 线段BD的长叫D到BC的距离 | D. | 在线段CA、CD、CB中,CD最短 |
1. 如图,△ABC中,AB=AC,AD⊥BC于D,DE⊥AB于E,DF⊥AC于F,下列结论:①DE=DF;②DA平分∠EDF;③AE=AF;④AD上的点到AB、AC两边距离相等.其中正确的有( )
如图,△ABC中,AB=AC,AD⊥BC于D,DE⊥AB于E,DF⊥AC于F,下列结论:①DE=DF;②DA平分∠EDF;③AE=AF;④AD上的点到AB、AC两边距离相等.其中正确的有( )
 如图,△ABC中,AB=AC,AD⊥BC于D,DE⊥AB于E,DF⊥AC于F,下列结论:①DE=DF;②DA平分∠EDF;③AE=AF;④AD上的点到AB、AC两边距离相等.其中正确的有( )
如图,△ABC中,AB=AC,AD⊥BC于D,DE⊥AB于E,DF⊥AC于F,下列结论:①DE=DF;②DA平分∠EDF;③AE=AF;④AD上的点到AB、AC两边距离相等.其中正确的有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
8.为了解某小区居民用水情况,随机抽查了10户家庭的月用水量,结果如下表,则关于这10户家庭月用水量数据组的说法,错误的是( )
| 月用水量(吨) | 4 | 5 | 6 |
| 户 数 | 3 | 4 | 3 |
| A. | 众数是5 | B. | 方差是4 | C. | 平均数是5 | D. | 中位数是5 |
5.估计$\sqrt{19}$的值( )
| A. | 在2到3之间 | B. | 在3到4之间 | C. | 在4到5之间 | D. | 在5到6之间 |