题目内容
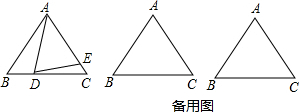
 如图,在平行四边形ABCD中,E为DC的中点,AE交BD于点F,S△DEF=12cm2,则S△AOB的值为( )
如图,在平行四边形ABCD中,E为DC的中点,AE交BD于点F,S△DEF=12cm2,则S△AOB的值为( )| A、12cm2 |
| B、24cm2 |
| C、36cm2 |
| D、48cm2 |
考点:相似三角形的判定与性质,平行四边形的性质
专题:
分析:根据平行四边形的性质得出AB=DC=2DE,OD=OB,DC∥AB,求出△DFE∽△BFA,推出
=
=
=
,
=(
)2=
,
=
=
,求出△AFB的面积是48cm2,△ADF的面积是24cm2,求出△ABD的面积即可.
| DE |
| AB |
| DF |
| BF |
| EF |
| FA |
| 1 |
| 2 |
| S△DEF |
| S△AFB |
| DE |
| AB |
| 1 |
| 4 |
| S△DEF |
| S△DFA |
| EF |
| AF |
| 1 |
| 2 |
解答:解:∵E为DC的中点,
∴DC=2DE,
∵四边形ABCD是平行四边形,
∴AB=DC=2DE,OD=OB,DC∥AB,
∴△DFE∽△BFA,
∴
=
=
=
,
=(
)2=(
)2=
,
=
=
,
∵S△DEF=12cm2,
∴△AFB的面积是48cm2,△ADF的面积是24cm2,
∴△ABD的面积是72cm2,
∵DO=OB,
∴△ADO和△ABO的面积相等,
∴S△AOB的值为
×72cm2=36cm2,
故选C.
∴DC=2DE,
∵四边形ABCD是平行四边形,
∴AB=DC=2DE,OD=OB,DC∥AB,
∴△DFE∽△BFA,
∴
| DE |
| AB |
| DF |
| BF |
| EF |
| FA |
| 1 |
| 2 |
| S△DEF |
| S△AFB |
| DE |
| AB |
| 1 |
| 2 |
| 1 |
| 4 |
| S△DEF |
| S△DFA |
| EF |
| AF |
| 1 |
| 2 |
∵S△DEF=12cm2,
∴△AFB的面积是48cm2,△ADF的面积是24cm2,
∴△ABD的面积是72cm2,
∵DO=OB,
∴△ADO和△ABO的面积相等,
∴S△AOB的值为
| 1 |
| 2 |
故选C.
点评:本题考查了相似三角形的性质和判定,平行四边形的性质的应用,解此题的关键是求出△AFB的面积和△ADF的面积.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
线段AB=5cm,BC=4cm,那么A、C两点的距离是( )
| A、1cm |
| B、9cm |
| C、1cm或9cm |
| D、以上答案都不对 |
下列计算正确的是( )
| A、(ab2)3=a3b5 |
| B、2m+3n=5mn |
| C、(a-b)(a+b)=a2-b2 |
| D、(a+b)2=a2+b2 |
 如图,AD∥EF∥BC,FG∥BD,和∠1相等的角有( )
如图,AD∥EF∥BC,FG∥BD,和∠1相等的角有( )| A、4个 | B、5个 | C、6个 | D、7个 |
 如图,与∠B是同旁内角的有( )
如图,与∠B是同旁内角的有( )| A、3个 | B、2个 | C、1个 | D、4个 |