题目内容
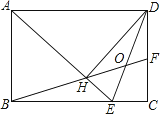
如图,在矩形ABCD中,AD=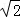 AB,∠BAD的平分线交BC于点E,DH⊥AE于点H,连接BH并延长交CD于点F,连接DE交BF于点O,下列结论:
AB,∠BAD的平分线交BC于点E,DH⊥AE于点H,连接BH并延长交CD于点F,连接DE交BF于点O,下列结论:
①∠AED=∠CED;②OE=OD;③BH=HF;④BC﹣CF=2HE;⑤AB=HF,
其中正确的有( )
A.2个 B.3个 C.4个 D.5个
C
【解析】∵在矩形ABCD中,AE平分∠BAD,∴∠BAE=∠DAE=45°,∴△ABE是等腰直角三角形,∴AE= AB,∵AD=
AB,∵AD= AB,∴AE=AD,又∠ABE=∠AHD=90°∴△ABE≌△AHD(AAS),∴BE=DH,∴AB=BE=AH=HD,∴∠ADE=∠AED=
AB,∴AE=AD,又∠ABE=∠AHD=90°∴△ABE≌△AHD(AAS),∴BE=DH,∴AB=BE=AH=HD,∴∠ADE=∠AED=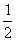 (180°﹣45°)=67.5°,
(180°﹣45°)=67.5°,
∴∠CED=180°﹣45°﹣67.5°=67.5°,∴∠AED=∠CED,故①正确;
∵∠AHB=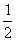 (180°﹣45°)=67.5°,∠OHE=∠AHB(对顶角相等),∴∠OHE=∠AED,
(180°﹣45°)=67.5°,∠OHE=∠AHB(对顶角相等),∴∠OHE=∠AED,
∴OE=OH,∵∠DOH=90°﹣67.5°=22.5°,∠ODH=67.5°﹣45°=22.5°,∴∠DOH=∠ODH,∴OH=OD,∴OE=OD=OH,故②正确;
∵∠EBH=90°﹣67.5°=22.5°,∴∠EBH=∠OHD,又BE=DH,∠AEB=∠HDF=45°
∴△BEH≌△HDF(ASA),∴BH=HF,HE=DF,故③正确;
由上述①、②、③可得CD=BE、DF=EH=CE,CF=CD-DF,∴BC-CF=(CD+HE)-(CD-HE)=2HE,所以④正确;
∵AB=AH,∠BAE=45°,∴△A BH不是等边三角形,∴AB≠BH,∴即AB≠HF,故⑤错误;
BH不是等边三角形,∴AB≠BH,∴即AB≠HF,故⑤错误;
综上所述,结论正确的是①②③④共4个.
故选C.

练习册系列答案
 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案
相关题目
 是实数,
是实数, ;
;
 的中点,连接AC、BC,则图中阴影部分面积是( )
的中点,连接AC、BC,则图中阴影部分面积是( )
 ﹣2
﹣2 B.
B. ﹣2
﹣2 ﹣
﹣ D.
D. ﹣
﹣ )÷(a﹣2+
)÷(a﹣2+ ),其中,a满足a﹣2=0.
),其中,a满足a﹣2=0. 有意义,则x应满足( )
有意义,则x应满足( ) B.x≤3且
B.x≤3且
 D.
D.
 无解,则m= .
无解,则m= .