题目内容
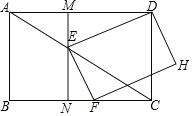
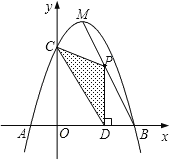
【题目】如图,抛物线y=﹣x2+bx+c与x轴相交于A、B两点,与y轴相交于点C,且点B与点C的坐标分别为B(3,0),C(0,3),点M是抛物线的顶点.
(1)求二次函数的关系式;
(2)点P为线段MB上一个动点,过点P作PD⊥x轴于点D.若OD=m,△PCD的面积为S,
①求S与m的函数关系式,写出自变量m的取值范围.
②当S取得最值时,求点P的坐标;
(3)在MB上是否存在点P,使△PCD为直角三角形?如果存在,请直接写出点P的坐标;如果不存在,请说明理由.
【答案】(1)y=﹣x2+2x+3;(2)①S=﹣m2+3m,1≤m≤3;②P(![]() ,3);(3)存在,点P的坐标为(
,3);(3)存在,点P的坐标为(![]() ,3)或(﹣3+3
,3)或(﹣3+3![]() ,12﹣6
,12﹣6![]() ).
).
【解析】
(1)将点B,C的坐标代入![]() 即可;
即可;
(2)①求出顶点坐标,直线MB的解析式,由PD⊥x轴且![]() 知P(m,﹣2m+6),即可用含m的代数式表示出S;
知P(m,﹣2m+6),即可用含m的代数式表示出S;
②在①的情况下,将S与m的关系式化为顶点式,由二次函数的图象及性质即可写出点P的坐标;
(3)分情况讨论,如图2﹣1,当![]() 时,推出
时,推出![]() ,则点P纵坐标为3,即可写出点P坐标;如图2﹣2,当
,则点P纵坐标为3,即可写出点P坐标;如图2﹣2,当![]() 时,证
时,证![]() ,由锐角三角函数可求出m的值,即可写出点P坐标;当
,由锐角三角函数可求出m的值,即可写出点P坐标;当![]() 时,不存在点P.
时,不存在点P.
(1)将点B(3,0),C(0,3)代入![]() ,
,
得 ![]() ,
,
解得![]() ,
,
∴二次函数的解析式为![]() ;
;
(2)①∵![]() ,
,
∴顶点M(1,4),
设直线BM的解析式为![]() ,
,
将点B(3,0),M(1,4)代入,
得![]() ,
,
解得 ![]() ,
,
∴直线BM的解析式为![]() ,
,
∵PD⊥x轴且![]() ,
,
∴P(m,﹣2m+6),
∴![]() ,
,
即![]() ,
,
∵点P在线段BM上,且B(3,0),M(1,4),
∴![]() ;
;
②∵![]() ,
,
∵![]() ,
,
∴当![]() 时,S取最大值
时,S取最大值![]() ,
,
∴P(![]() ,3);
,3);
(3)存在,理由如下:
①如图2﹣1,当![]() 时,
时,
∵![]() ,
,
∴四边形CODP为矩形,
∴![]() ,
,
将![]() 代入直线
代入直线![]() ,
,
得![]() ,
,![]()
∴P(![]() ,3);
,3);
②如图2﹣2,当∠PCD=90°时,
∵![]() ,
,![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴ ,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
解得![]()
![]() (舍去),
(舍去),![]() ,
,
∴P(![]() ,
,![]() ),
),
③当![]() 时,
时,
∵PD⊥x轴,
∴不存在,
综上所述,点P的坐标为(![]() ,3)或(
,3)或(![]() ,
,![]() ).
).




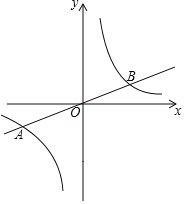
【题目】已知![]() 是
是![]() 的反比例函数,下表给出了
的反比例函数,下表给出了![]() 与
与![]() 的一些值.
的一些值.
| … | -4 | -2 | -1 | 1 | 3 | 4 | … | ||
| … | -2 | 6 | 3 | … |
(1)求出这个反比例函数的表达式;
(2)根据函数表达式完成上表;
(3)根据上表,在下图的平面直角坐标系中作出这个反比例函数的图象.