Question

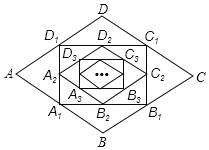
【题目】如图，在菱形ABCD中，边长为1，∠A＝60，顺次连接菱形ABCD各边中点，可得四边形A1B1C1D1；顺次连结四边形A1B1C1D1各边中点，可得四边形A2B2C2D2；顺次连结四边形A2B2C2D2各边中点，可得四边形A3B3C3D3；按此规律继续下去，…，则四边形A2019B2019C2019D2019的面积是_____．

Answer 1

【答案】

【解析】

连接AC、BD，根据菱形的面积公式，得S菱形ABCD=，进而得矩形A1B1C1D1的面积，菱形A2B2C2D2的面积，以此类推，即可得到答案．

连接AC、BD，则AC⊥BD，

∵菱形ABCD中，边长为1，∠A＝60°，

∴S菱形ABCD＝ACBD＝1×1×sin60°＝，

∵顺次连结菱形ABCD各边中点，可得四边形A1B1C1D1，

∴四边形A1B1C1D1是矩形，

∴矩形A1B1C1D1的面积＝ACBD＝ACBD＝S菱形ABCD＝＝，

菱形A2B2C2D2的面积＝×矩形A1B1C1D1的面积＝S菱形ABCD＝＝，

……，

∴四边形A2019B2019C2019D2019的面积＝，

故答案为：．