题目内容
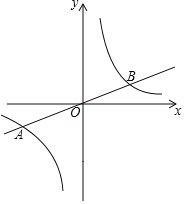
【题目】如图,正比例函数![]() 的图象与反比例函数
的图象与反比例函数![]() 的图象交于
的图象交于![]() 、
、![]() 两点.
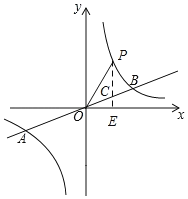
两点.![]() 是第一象限内反比例函数图象上一点,过点
是第一象限内反比例函数图象上一点,过点![]() 作
作![]() 轴的平行线,交直线
轴的平行线,交直线![]() 于点
于点![]() ,连接
,连接![]() ,若
,若![]() 的面积为
的面积为![]() ,则点
,则点![]() 的坐标为_____________.
的坐标为_____________.
【答案】![]() 或(2,4)
或(2,4)
【解析】
把A(a,﹣2)代入y![]() x,可得A(﹣4,﹣2),把A(﹣4,﹣2)代入y
x,可得A(﹣4,﹣2),把A(﹣4,﹣2)代入y![]() ,可得反比例函数的表达式为y
,可得反比例函数的表达式为y![]() ,过P作PE⊥x轴于E,交AB于C,先设P(m,
,过P作PE⊥x轴于E,交AB于C,先设P(m,![]() ),则C(m,
),则C(m,![]() m),根据△POC的面积为3,可得方程
m),根据△POC的面积为3,可得方程![]() m×|
m×|![]() m
m![]() |=3,求得m的值,即可得到点P的坐标.
|=3,求得m的值,即可得到点P的坐标.
把A(a,﹣2)代入y![]() x,可得:a=﹣4,
x,可得:a=﹣4,
∴A(﹣4,﹣2),
把A(﹣4,﹣2)代入y![]() ,可得:k=8,
,可得:k=8,
∴反比例函数的表达式为y![]() .
.
如图所示,过P作PE⊥x轴于E,交AB于C,设P(m,![]() ),其中m>0,则C(m,
),其中m>0,则C(m,![]() m).
m).
∵△POC的面积为3,
∴![]() m×|
m×|![]() m
m![]() |=3,
|=3,
解得:m=2![]() 或2,
或2,
∴P(2![]() ,
,![]() )或(2,4).
)或(2,4).
故答案为:(![]() ,
,![]() )或(2,4).
)或(2,4).

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案
相关题目