题目内容
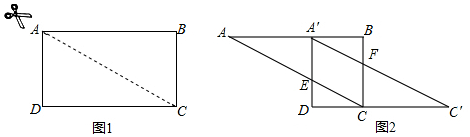
16.如图1,平行四边形ABCD中,点E为AD的中点,连CE,点M、N为CE上两点,且BM∥DN,
(1)求证:△BCM∽∠DEN;
(2)如图2,连DM并延长交AB于F,若BF=2AF,求$\frac{DM}{MF}$的值;
(3)在(2)的条件下,连BN,求S△BFM:S四边形BMDN的值.
分析 (1)利用平行线的性质得出∠DEN=∠BCM,∠END=∠CMB,即可得出结论,
(2)先判断出BM=2DN,再取BF、BM的中点H、Q,连接HQ、AQ,则HQ是三角形的中位线,所以MF=2QH,根据BF=2AF,得出AF=HF,得出PF是△AQH的中位线,得出QH=2PF,MF=2QH=4PF,PM=3PF,同理:求得DM=PM=3PF,即可求得$\frac{DM}{MF}$的值;
(3)连接BD,作BH⊥DN于H,先求得$\frac{{S}_{△BDM}}{{S}_{△BMF}}=\frac{3}{4}$,得出S△BMF=$\frac{4}{3}$S△BDM,进而得出$\frac{{S}_{△BDN}}{{S}_{△BDM}}=\frac{\frac{1}{2}DN•BH}{\frac{1}{2}BM•BH}$=$\frac{DN}{BM}=\frac{1}{2}$,得出S△BDM=2S△BDN,从而得出S梯形BMDN=S△BDN+S△BDM=3S△BDN,即可求得$\frac{{S}_{△BFM}}{{S}_{四边形BMDN}}$的值,
解答 (1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠DEN=∠BCM,
又∵BM∥DN,
∴∠END=∠CMB,
∴△EDN∽△CBM,
﹙2﹚∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,
∴DE=$\frac{1}{2}$CB,
由(1)知,△EDN∽△CBM,
∴$\frac{DE}{BC}=\frac{DN}{BM}=\frac{1}{2}$,
∴BM=2DN;
如图2, 取BF、BM的中点H、Q,连接HQ、AQ,
取BF、BM的中点H、Q,连接HQ、AQ,
∵BQ=MQ,BH=HF,
∴QH∥DF,
∴MF=2QH,
∵BF=2AF,
∴AF=HF,
∴PF是△AQH的中位线,
∴QH=2PF,
∴MF=2QH=4PF,
∴PM=3PF,
同理:EM是△ADP的中位线,
∴DM=PM=3PF,
∴$\frac{DM}{MF}=\frac{3PF}{4PF}=\frac{3}{4}$.
(3)如图3,连接BD,作BH⊥DN于H,
∵BM∥DN,
∴BH⊥BM,
∵$\frac{DM}{MF}=\frac{3}{4}$,
∴$\frac{{S}_{△BDM}}{{S}_{△BMF}}=\frac{3}{4}$,
∴S△BMF=$\frac{4}{3}$S△BDM,
∵BM∥DN,
∴$\frac{{S}_{△BDN}}{{S}_{△BDM}}=\frac{\frac{1}{2}DN•BH}{\frac{1}{2}BM•BH}$=$\frac{DN}{BM}=\frac{1}{2}$,
∴S△BDM=2S△BDN,
∴S梯形BMDN=S△BDN+S△BDM=3S△BDN,
∴S△BMF=$\frac{4}{3}$S△BDM=$\frac{8}{3}$S△BDN,
∴$\frac{{S}_{△BFM}}{{S}_{四边形BMDN}}$=$\frac{\frac{8}{3}{S}_{△BDN}}{3{S}_{△BDN}}$=$\frac{8}{9}$.
点评 此题是相似三角形的综合题,主要考查了平行四边形的性质,三角形的中位线定理,三角形相似的判定和性质,以及三角形的面积等,解(2)的关键是判断出BM=2DN,解(3)的关键是S△BMF=$\frac{4}{3}$S△BDM,是一道中等难度的中考常考题.

 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案 如图,把含30°角的直角三角板的直角顶点C放在直线a上,其中∠A=30°,直角边AC和斜边AB分别与直线b相交,如果a∥b,且∠1=25°,则∠2的度数为( )
如图,把含30°角的直角三角板的直角顶点C放在直线a上,其中∠A=30°,直角边AC和斜边AB分别与直线b相交,如果a∥b,且∠1=25°,则∠2的度数为( )| A. | 20° | B. | 25° | C. | 30° | D. | 35° |
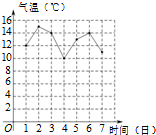 如图是我市4月1日至7日一周内“日平均气温变化统计图”,在这组数据中,众数和中位数分别是( )
如图是我市4月1日至7日一周内“日平均气温变化统计图”,在这组数据中,众数和中位数分别是( )| A. | 13,13 | B. | 14,10 | C. | 14,13 | D. | 13,14 |
 在哈市地铁2号线的建设中,甲、乙两个建设公司同时挖掘两段长度相等的隧道,如图是甲、乙两公司挖掘隧道长度y(米)与挖掘时间x(时)之间关系的部分图象.如果甲队施工速度始终不变,乙队在开挖6小时后,施工速度每小时增加了7米,结果两队同时完成了任务,那么甲队从开挖到完工所挖隧道的总长度为( )米.
在哈市地铁2号线的建设中,甲、乙两个建设公司同时挖掘两段长度相等的隧道,如图是甲、乙两公司挖掘隧道长度y(米)与挖掘时间x(时)之间关系的部分图象.如果甲队施工速度始终不变,乙队在开挖6小时后,施工速度每小时增加了7米,结果两队同时完成了任务,那么甲队从开挖到完工所挖隧道的总长度为( )米.| A. | 100 | B. | 110 | C. | 120 | D. | 130 |
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{6}$ |
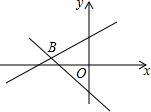 一次函数y=ax+3与y=bx-1的图象如图所示,其交点B(-3,m),则不等式ax-bx+3>-1的解集表示在数轴上正确的是( )
一次函数y=ax+3与y=bx-1的图象如图所示,其交点B(-3,m),则不等式ax-bx+3>-1的解集表示在数轴上正确的是( )


