题目内容
5.为降低空气污染,公交公司决定全部更换节能环保的燃气公交车.计划购买A型和B型两种公交车共10辆,其中每台的价格,年均载客量如表:| A型 | B型 | |
| 价格(万元/辆) | a | b |
| 年均载客量(万人/年/辆) | 60 | 100 |
(1)求购买每辆A型公交车和每辆B型公交车分别多少万元?
(2)如果该公司购买A型和B型公交车的总费用不超过1200万元,且确保这10辆公交车年均载客总和不少于680万人次,有哪几种购车方案?请你设计一个方案,使得购车总费用最少.
分析 (1)根据“购买A型公交车1辆,B型公交车2辆,共需400万元;若购买A型公交车2辆,B型公交车1辆,共需350万元”列方程组求解可得;
(2)设购买A型公交车x辆,则购买B型公交车(10-x)辆,根据“总费用不超过1200万元、年均载客总和不少于680万人次”求得x的范围,设购车的总费用为W,列出W关于x的函数解析式,利用一次函数的性质求解可得.
解答 解:(1)根据题意,得:$\left\{\begin{array}{l}{a+2b=400}\\{2a+b=350}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{a=100}\\{b=150}\end{array}\right.$,
答:购买每辆A型公交车100万元,购买每辆B型公交车150万元;
(2)设购买A型公交车x辆,则购买B型公交车(10-x)辆,
根据题意得:$\left\{\begin{array}{l}{100x+150(10-x)≤1200}\\{60x+100(10-x)≥680}\end{array}\right.$,
解得:6≤x≤8,
设购车的总费用为W,
则W=100x+150(10-x)=-50x+1500,
∵W随x的增大而减小,
∴当x=8时,W取得最小值,最小值为1100万元.
点评 本题主要考查二元一次方程组、一元一次不等式组及一次函数的应用,解题的关键是根据题意确定相等关系或不等式关系以列出方程组和不等式组是解题的关键.

练习册系列答案
相关题目
16.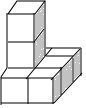 如图,由8个大小相同的正方体搭成的几何体,则关于它的视图说法正确的是( )
如图,由8个大小相同的正方体搭成的几何体,则关于它的视图说法正确的是( )
 如图,由8个大小相同的正方体搭成的几何体,则关于它的视图说法正确的是( )
如图,由8个大小相同的正方体搭成的几何体,则关于它的视图说法正确的是( )| A. | 正视图的面积最大 | B. | 左视图的面积最大 | ||
| C. | 俯视图的面积最大 | D. | 三个视图的面积一样大 |




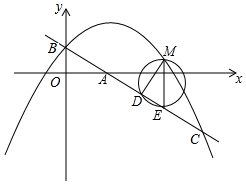 在平面直角坐标系中,直线y=-$\frac{3}{4}$x+1交y轴于点B,交x轴于点A,抛物线y=-$\frac{1}{2}$x2+bx+c经过点B,与直线y=-$\frac{3}{4}$x+1交于点C(4,-2).
在平面直角坐标系中,直线y=-$\frac{3}{4}$x+1交y轴于点B,交x轴于点A,抛物线y=-$\frac{1}{2}$x2+bx+c经过点B,与直线y=-$\frac{3}{4}$x+1交于点C(4,-2). 如图,在?ABCD中,AE,BF分别平分∠DAB,∠ABC,交CD于点E,F(点E在F的右边),若AD=5,EF=2,则AB的长是8.
如图,在?ABCD中,AE,BF分别平分∠DAB,∠ABC,交CD于点E,F(点E在F的右边),若AD=5,EF=2,则AB的长是8.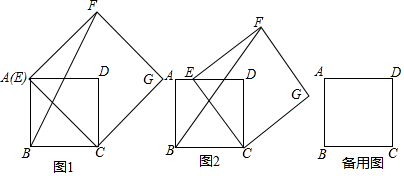
 如图,直线y=-$\frac{\sqrt{3}}{3}$x-$\sqrt{3}$与x,y轴分别交于点A,B,与反比例函数y=$\frac{k}{x}$的图象在第二象限交于点C,过点A作x轴的垂线交该反比例函数图象于点D.若AD=AC,则点D的坐标为(-3,2$\sqrt{3}$).
如图,直线y=-$\frac{\sqrt{3}}{3}$x-$\sqrt{3}$与x,y轴分别交于点A,B,与反比例函数y=$\frac{k}{x}$的图象在第二象限交于点C,过点A作x轴的垂线交该反比例函数图象于点D.若AD=AC,则点D的坐标为(-3,2$\sqrt{3}$). 如图,有一正方体的房间,在房间内的一角A处由一只蚂蚁,它想到房间的另一角B处去吃食物,请问它采取怎样的行走路线是最近的?如果一只蜜蜂,要从A到B怎样飞是最近的?请你画图展示.
如图,有一正方体的房间,在房间内的一角A处由一只蚂蚁,它想到房间的另一角B处去吃食物,请问它采取怎样的行走路线是最近的?如果一只蜜蜂,要从A到B怎样飞是最近的?请你画图展示.