题目内容
10. 如图,在?ABCD中,AE,BF分别平分∠DAB,∠ABC,交CD于点E,F(点E在F的右边),若AD=5,EF=2,则AB的长是8.
如图,在?ABCD中,AE,BF分别平分∠DAB,∠ABC,交CD于点E,F(点E在F的右边),若AD=5,EF=2,则AB的长是8.
分析 由AB∥CD,得∠DEA=∠EAB,再由角平分线的定义得出∠DAE=∠EAB,从而得出∠DAE=∠DEA,即DA=DE=5,同理得出CF=CB=5,即可得出答案.
解答 解:∵四边形ABCD是平行四边形,
∴AD=BC=5,AB=DC,AB∥DC,
∵AE平分∠DAB,
∴∠DAE=∠BAE,
∵AB∥DC,
∴∠DEA=∠BAE,
∴∠DAE=∠DEA,
∴AD=DE=5,
同理BC=CF=5,
∴AB=CD=DE+CF-EF=5+5-2=8;
故答案为:8.
点评 本题考查了平行四边形的性质、角平分线的性质以及等腰三角形的判定和性质,证明AD=DE,BC=CF是解决问题的关键.

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目
1. 如图,已知,点A(0,0)、B(4$\sqrt{3}$,0)、C(0,4),在△ABC内依次作等边三角形,使一边在x轴上,另一个顶点在BC边上,作出的等边三角形分别是第1个△AA1B1,第2个△B1A2B2,第3个△B2A3B3,…则第2017个等边三角形的边长等于( )
如图,已知,点A(0,0)、B(4$\sqrt{3}$,0)、C(0,4),在△ABC内依次作等边三角形,使一边在x轴上,另一个顶点在BC边上,作出的等边三角形分别是第1个△AA1B1,第2个△B1A2B2,第3个△B2A3B3,…则第2017个等边三角形的边长等于( )
 如图,已知,点A(0,0)、B(4$\sqrt{3}$,0)、C(0,4),在△ABC内依次作等边三角形,使一边在x轴上,另一个顶点在BC边上,作出的等边三角形分别是第1个△AA1B1,第2个△B1A2B2,第3个△B2A3B3,…则第2017个等边三角形的边长等于( )
如图,已知,点A(0,0)、B(4$\sqrt{3}$,0)、C(0,4),在△ABC内依次作等边三角形,使一边在x轴上,另一个顶点在BC边上,作出的等边三角形分别是第1个△AA1B1,第2个△B1A2B2,第3个△B2A3B3,…则第2017个等边三角形的边长等于( )| A. | $\frac{\sqrt{3}}{{2}^{2015}}$ | B. | $\frac{\sqrt{3}}{{2}^{2016}}$ | C. | $\frac{\sqrt{3}}{{2}^{2017}}$ | D. | $\frac{\sqrt{3}}{{2}^{2019}}$ |
5.为降低空气污染,公交公司决定全部更换节能环保的燃气公交车.计划购买A型和B型两种公交车共10辆,其中每台的价格,年均载客量如表:
若购买A型公交车1辆,B型公交车2辆,共需400万元;若购买A型公交车2辆,B型公交车1辆,共需350万元
(1)求购买每辆A型公交车和每辆B型公交车分别多少万元?
(2)如果该公司购买A型和B型公交车的总费用不超过1200万元,且确保这10辆公交车年均载客总和不少于680万人次,有哪几种购车方案?请你设计一个方案,使得购车总费用最少.
| A型 | B型 | |
| 价格(万元/辆) | a | b |
| 年均载客量(万人/年/辆) | 60 | 100 |
(1)求购买每辆A型公交车和每辆B型公交车分别多少万元?
(2)如果该公司购买A型和B型公交车的总费用不超过1200万元,且确保这10辆公交车年均载客总和不少于680万人次,有哪几种购车方案?请你设计一个方案,使得购车总费用最少.
19.下列说法中正确的是( )
| A. | 8的立方根是±2 | |
| B. | $\sqrt{8}$是一个最简二次根式 | |
| C. | 函数y=$\frac{1}{x-1}$的自变量x的取值范围是x>1 | |
| D. | 在平面直角坐标系中,点P(2,3)与点Q(-2,3)关于y轴对称 |
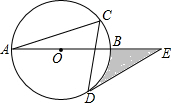 如图,⊙O的半径是4,圆周角∠C=60°,点E时直径AB延长线上一点,且∠DEB=30°,则图中阴影部分的面积为8$\sqrt{3}$-$\frac{8π}{3}$.
如图,⊙O的半径是4,圆周角∠C=60°,点E时直径AB延长线上一点,且∠DEB=30°,则图中阴影部分的面积为8$\sqrt{3}$-$\frac{8π}{3}$.