题目内容
如图,A、D、F、B在同一直线上,AD=BF,AE=BC,且AE∥BC.
求证:(1)EF=CD;(2)EF∥CD.

【考点】全等三角形的判定与性质;平行线的判定与性质.
【专题】证明题.
【分析】(1)要证EF=CD就证△AEF≌△BCD,由已知得AE∥BC,所以∠A=∠B.又因AD=BF,所以AF=AD+DF=BF+FD=BD,又因AE=BC,所以△AEF≌△BCD.
(2)再根据全等即可求出EF∥CD.
【解答】证明:(1)∵AE∥BC,
∴∠A=∠B.
又∵AD=BF,
∴AF=AD+DF=BF+FD=BD.
又∵AE=BC,
在△AEF与△BCD中,
∵
∴△AEF≌△BCD,
∴EF=CD.
(2)∵△AEF≌△BCD,
∴∠EFA=∠CDB.
∴EF∥CD.
【点评】本题考查全等三角形和平行线的判定及推理论证能力,已知中有平行线能为证全等提供角相等的条件,而全等又能得到角相等从而为平行线的证明提供了条件.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目


 ,P2,连接P1P2交OA于M,交OB于N,P1P2=15,则△PMN的周长为__________.
,P2,连接P1P2交OA于M,交OB于N,P1P2=15,则△PMN的周长为__________.


 .16 B.18 C.26 D.28
.16 B.18 C.26 D.28 方形ABCD四边运动,求经过多长时间点P与点Q第一次在正方形ABCD边上的何处相遇?
方形ABCD四边运动,求经过多长时间点P与点Q第一次在正方形ABCD边上的何处相遇?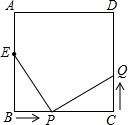
 的值为0.
的值为0.