Question

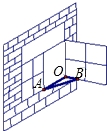
如图所示，点P为∠AOB内一点，分别作出P点关于OA、OB的对称点P₁，P₂，连接P₁P₂交OA于M，交OB于N，P₁P₂=15，则△PMN的周长为__________．

Answer 1

15．

【考点】轴对称的性质．

【分析】P点关于OA的对称是点P₁，P点关于OB的对称点P₂，故有PM=P₁M，PN=P₂N．

【解答】解：∵P点关于OA的对称是点P₁，P点关于OB的对称点P₂，

∴PM=P₁M，PN=P₂N．

∴△PMN的周长为PM+PN+MN=MN+P₁M+P₂N=P₁P₂=15．

故答案为：15

【点评】本题考查轴对称的性质．对应点的连线与对称轴的位置关系是互相垂直，对应点所连的线段被对称轴垂直平分，对称轴上的任何一点到两个对应点之间的距离相等，对应的角、线段都相等．