题目内容
13.解不等式(组)(1)1+$\frac{x}{2}$>$\frac{x-2}{4}$;
(2)$\left\{\begin{array}{l}2x+4≤5(x+2)\\ x-1<\frac{2x}{3}\end{array}\right.$,并把解集在数轴上表示出来.
分析 (1)先去分母,再移项、合并同类项即可;
(2)分别求出各不等式的解集,再求出其公共解集,并在数轴上表示出来即可;
解答 解:(1)去分母得,4+2x>x-2,
移项得,2x-x>-4-2,
合并同类项得,x>-6.
(2)$\left\{\begin{array}{l}2x+4≤5(x+2)①\\ x-1<\frac{2x}{3}②\end{array}\right.$,
由①得:x≥-2,由②得:x<3.
故不等式组的解集为:-2≤x<3.
在数轴上表示为: .
.
点评 本题考查的是解一元一次不等式组,熟知“同大取大;同小取小;大小小大中间找;大大小小找不到”的法则是解答此题的关键.

练习册系列答案
 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案
相关题目
3.人类的遗传物质是DNA,DNA是一个很长的链,最短的22号染色体也长达30000000个核苷酸,30000000用科学记数法表示为( )
| A. | 3×107 | B. | 30×106 | C. | 0.3×107 | D. | 0.3×108 |
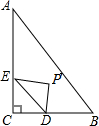 如图,∠C=90°,BC=3,AB=5,点D是BC上一动点,CD=x,DE∥AB交AC于点E,以直线DE为轴作△CDE的轴对称△PDE,△PDE落在△ABC内的面积为y,则下列能刻画y与x之间函数关系的图象是( )
如图,∠C=90°,BC=3,AB=5,点D是BC上一动点,CD=x,DE∥AB交AC于点E,以直线DE为轴作△CDE的轴对称△PDE,△PDE落在△ABC内的面积为y,则下列能刻画y与x之间函数关系的图象是( )