Question

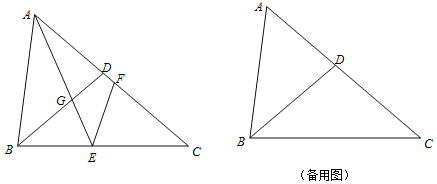
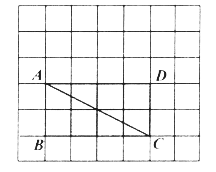
【题目】已知：在△ABC中AB＝AC，点D为BC边的中点，点F是AB边上一点，点E在线段DF的延长线上，∠BAE＝∠BDF，点M在线段DF上，∠ABE＝∠DBM．

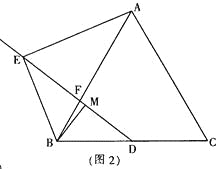
1.如图1，当∠ABC＝45°时，求证：AE＝MD；

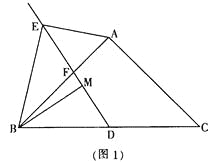
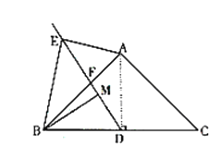
2.如图2，当∠ABC＝60°时，则线段AE、MD之间的数量关系为： ．

3.在（2）的条件下延长BM到P，使MP＝BM，连接CP，若AB＝7，AE＝，求tan∠ACP的值．

Answer 1

【答案】(1)证明见解析；（2）AE=2MD；（3）tan∠ACP= .

【解析】

(1）由题意知∠BAE=∠BDM，∠ABE=∠DBM故有△ABE∽△DBMAE：DM=AB：BD，而∠ABC=45°AB=BD，则有AE=MD；

（2）由于△ABE∽△DBM，相似比为2，进而确定出AE与DM的关系；
（3）由题意知得△BEP为等边三角形，有EM⊥BP，∠BMD=∠AEB=90°，在Rt△AEB中求得AE、AB、tan∠EAB的值，由D为BC中点，M为BP中点，得DM∥PC，求得tan∠PCB的值，在Rt△ABD和Rt△NDC中，由锐角三角函数的定义求得AD、ND的值，进而求得tan∠ACP的值．

(1)证明：如图1 连接AD

∵AB=AC，BD=CD，

∴AD⊥BC，

又∵∠ABC=45°，

∴BD=ABcos∠ABC，即AB= BD．

∵∠BAE=∠BDM，∠ABE=∠DBM，

∴△ABE∽△DBM

∴,

∴AE=MD．

（2）AE=2MD

如图2，连接AD，EP，过N作NH⊥AC，垂足为H，连接NH，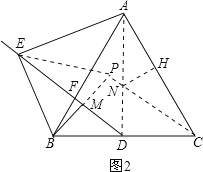

∵AB=AC，∠ABC=60°，

∴△ABC是等边三角形，

又∵D为BC的中点，

∴AD⊥BC，∠DAC=30°，BD=DC=AB，

∵∠BAE=∠BDM，∠ABE=∠DBM，

∴△ABE∽△DBM，
∴，即AE=2DM；

（3）解：如图2 由（2）得△ABE∽△DBM，

∴，∠AEB=∠DMB，

∴EB=2BM，

又∵BM=MP

∴EB=BP，

又∵∠EBM=∠ABC=60°，

∴△BEP为等边三角形，

∴EM⊥BP，

∴∠BMD=90° ，

∴∠AEB=90°，

在Rt△AEB中，AE=2，AB=7，

∴=，

∵D为BC中点 M为PB中点，

∴DM//PC，

∴∠MDB=∠PCB，

∴∠EAB=∠PCB，

∴tan∠PCB=，

在RT△ABD中，AD=ABsin∠ABD=，

在RT△NDC中，ND=CDtan∠NCD ==，

∴NA=AD-ND=，

过N作NH⊥AC，垂足为H，

在RT△ANH中，NH=AH=,AH=ANcos∠NAH=，

∴CH=AC-AH=，

∴tan∠ACP==．