题目内容
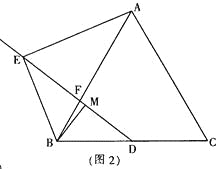
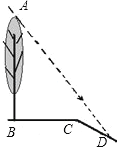
【题目】如图,坡面CD的坡比为![]() ,坡顶的平地BC上有一棵小树AB,当太阳光线与水平线夹角成60°时,测得小树的在坡顶平地上的树影BC=3米,斜坡上的树影CD=
,坡顶的平地BC上有一棵小树AB,当太阳光线与水平线夹角成60°时,测得小树的在坡顶平地上的树影BC=3米,斜坡上的树影CD=![]() 米,则小树AB的高是 .
米,则小树AB的高是 .
【答案】4![]() 米.
米.
【解析】
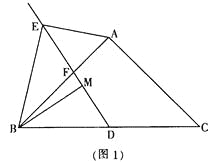
试题分析:此题是把实际问题转化为解直角三角形问题,首先根据题意作图(如图),得Rt△AFD,Rt△CED,然后由Rt△CED,和坡面CD的坡比为![]() ,求出CE和ED,再由Rt△AFD和三角函数求出AF.进而求出AB.
,求出CE和ED,再由Rt△AFD和三角函数求出AF.进而求出AB.
解:由已知得Rt△AFD,Rt△CED,如图,且得:∠ADF=60°,FE=BC,BF=CE,
在Rt△CED中,设CE=x,由坡面CD的坡比为![]() ,得:
,得:
DE=![]() x,则根据勾股定理得:
x,则根据勾股定理得:
x2+![]() =
=![]() ,
,
得x=±![]() ,﹣
,﹣![]() 不合题意舍去,
不合题意舍去,
所以,CE=![]() 米,则,ED=
米,则,ED=![]() 米,
米,
那么,FD=FE+ED=BC+ED=3+![]() =
=![]() 米,
米,
在Rt△AFD中,由三角函数得:
![]() =tan∠ADF,
=tan∠ADF,
∴AF=FDtan60°=![]() ×
×![]() =
=![]() 米,
米,
∴AB=AF﹣BF=AF﹣CE=![]() ﹣
﹣![]() =4
=4![]() 米,
米,
故答案为:4![]() 米.
米.


练习册系列答案
相关题目