Question

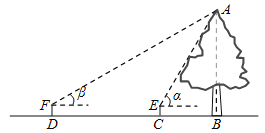
【题目】如图，AB是一棵古树，某校初四(1)班数学兴趣小组的同学想利用所学知识测出这棵古树的高，过程如下：在古树同侧的水平地面上，分别选取了C、D两点(C、D两点与古树在同一直线上)，用测角仪在C处测得古树顶端A的仰角α＝60°，在D处测得古树顶端A的仰角β＝30°，又测得C、D两点相距14米．已知测角仪高为1.5米，请你根据他们所测得的数据求出古树AB的高．(精确到0.1米，≈1.732)

Answer 1

【答案】AB的高约为13.6米．

【解析】

如图，连接FE并延长交AB于G，则易得FE=CD=14米，GB=FD=1.5米，由三角形的外角性质和和等腰三角形的判定可得AE=FE，然后根据解直角三角形的知识可求出AG的长，而AB＝AG+GB，进而可得结果．

解：如图，连接FE并延长交AB于G，则FG⊥AB，四边形FDBG、CDFE是矩形，FE=CD=14米，GB=FD=EC=1.5米，

∵∠AEG=α＝60°，∠AFE=β＝30°，∴∠FAE=30°，∴∠AFE=∠FAE，∴AE=FE=14米，

在Rt△AEG中，∵sinα=，∴．

∴AB＝AG+GB=+1.5≈13.6米．

即古树AB的高约为13.6米．