题目内容
已知S=1+2-1+2-2+2-3+…+2-2006,请计算右边的算式,求出S的值.
考点:负整数指数幂
专题:
分析:首先把S=1+2-1+2-2+2-3+…+2-2006,乘以2可得2S=S=2(1+2-1+2-2+2-3+…+2-2006)=2+1+2-1+2-2+2-3+…+2-2005 ,再把两式相减即可.
解答:解:∵S=1+2-1+2-2+2-3+…+2-2006 ①,
∴2S=S=2(1+2-1+2-2+2-3+…+2-2006)=2+1+2-1+2-2+2-3+…+2-2005 ②,
②-①得:S=2-2-2006=2-
=
=
.
∴2S=S=2(1+2-1+2-2+2-3+…+2-2006)=2+1+2-1+2-2+2-3+…+2-2005 ②,
②-①得:S=2-2-2006=2-
| 1 |
| 22006 |
| 2×22006-1 |
| 22006 |
| 22007-1 |
| 22006 |
点评:此题主要考查了负整数指数幂,关键是掌握负整数指数为正整数指数的倒数.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 已知,在△ABC中,DE∥BC,F是AB上一点,FE的延长线交BC的延长线于点G,则∠EGH与∠ADE的大小有什么关系?请说明理由.
已知,在△ABC中,DE∥BC,F是AB上一点,FE的延长线交BC的延长线于点G,则∠EGH与∠ADE的大小有什么关系?请说明理由.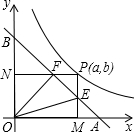 如图,在平面直角坐标系中,直线y=-x+
如图,在平面直角坐标系中,直线y=-x+ 如图,在△ABC中,AD是BC边上的中线,E是AD的中点,过点A作AF∥BC,交BE的延长线于点F,连结CF.
如图,在△ABC中,AD是BC边上的中线,E是AD的中点,过点A作AF∥BC,交BE的延长线于点F,连结CF.