题目内容
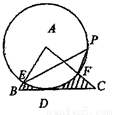
如图,在△ABC中,∠C=90°, AD是∠BAC的平分线,O是AB上一点, 以 OA为半径的⊙O经过点D。

(1)求证: BC是⊙O切线;
(2)若BD=5, DC=3, 求AC的长。
(1)证明见解析;(2)6.
【解析】
试题分析:(1)要证BC是⊙O的切线,只要连接OD,再证OD⊥BC即可.
(2)过点D作DE⊥AB,根据角平分线的性质可知CD=DE=3,由勾股定理得到BE的长,再通过证明△BDE∽△BAC,根据相似三角形的性质得出AC的长.
试题解析:(1)证明:连接OD;

∵AD是∠BAC的平分线,
∴∠1=∠3.
∵OA=OD,
∴∠1=∠2.
∴∠2=∠3.
∴OD∥AC.
∴∠ODB=∠ACB=90°.
∴OD⊥BC.
∴BC是⊙O切线.
(2)【解析】
过点D作DE⊥AB,

∵AD是∠BAC的平分线,
∴CD=DE=3.
在Rt△BDE中,∠BED=90°,
由勾股定理得:BE=
∵∠BED=∠ACB=90°,∠B=∠B,
∴△BDE∽△BAC.
∴ .
.
∴ .
.
∴AC=6.
考点:切线的判定.

练习册系列答案
 导学全程练创优训练系列答案
导学全程练创优训练系列答案
相关题目

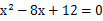 的一个实数根,则这个三角形的周长为( )
的一个实数根,则这个三角形的周长为( ) ,正方形
,正方形 的四个顶点分别在
的四个顶点分别在 上,
上, 过点D且垂直于
过点D且垂直于 于点E,分别交
于点E,分别交 于点F,G,
于点F,G, .
.
 ,正方形
,正方形 绕点A顺时针旋转得到
绕点A顺时针旋转得到 ,旋转角为
,旋转角为 ,点
,点 在直线
在直线 上,以
上,以 为边在的
为边在的 左侧作菱形
左侧作菱形 ,使点
,使点 分别在直线
分别在直线
 与
与 的函数关系并给出证明;②若
的函数关系并给出证明;②若 ,求菱形
,求菱形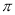 )
)