题目内容
如图1,有一组平行线 ,正方形
,正方形 的四个顶点分别在
的四个顶点分别在 上,
上, 过点D且垂直于
过点D且垂直于 于点E,分别交
于点E,分别交 于点F,G,
于点F,G, .
.

(1) ,正方形
,正方形 的边长= ;
的边长= ;
(2)如图2,将 绕点A顺时针旋转得到
绕点A顺时针旋转得到 ,旋转角为
,旋转角为 ,点
,点 在直线
在直线 上,以
上,以 为边在的
为边在的 左侧作菱形
左侧作菱形 ,使点
,使点 分别在直线
分别在直线 上.
上.

①写出 与
与 的函数关系并给出证明;②若
的函数关系并给出证明;②若 ,求菱形
,求菱形 的边长.
的边长.
(1)1, ;(2)
;(2) .
.
【解析】
试题分析:(1)利用已知得出△AED≌△DGC(AAS),即可得出AE,以及正方形的边长;
(2)①过点B′作B′M垂直于l1于点M,进而得出Rt△AED′≌Rt△B′MA(HL),求出∠B′AD′与α的数量关系即可;
②首先过点E作ON垂直于l1分别交l1,l2于点O,N,若α=30°,则∠ED′N=60°,可求出AE=1,EO,EN,ED′的长,进而由勾股定理可知菱形的边长.
试题解析:(1)由题意可得:∠1+∠3=90°,∠1+∠2=90°,
∴∠2=∠3,
在△AED和△DGC中,
 ,
,
∴△AED≌△DGC(AAS),
∴AE=GD=1,
又∵DE=1+2=3,
∴正方形ABCD的边长= ,
,
(2)①∠B′AD′=90°-α;
理由:过点B′作B′M垂直于l1于点M,

在Rt△AED′和Rt△B′MA中,
 ,
,
∴Rt△AED′≌Rt△B′MA(HL),
∴∠D′AE+∠B′AM=90°,
∠B′AD′+α=90°,
∴∠B′AD′=90°-α;
②过点E作ON垂直于l1分别交l1,l3于点O,N,
若α=30°,
则∠ED′N=60°,AE=1,
故EO= ,EN=
,EN= ,ED′=
,ED′= ,
,
由勾股定理可知菱形的边长为: .
.
考点:1.几何变换综合题;2.全等三角形的判定与性质;3.勾股定理的应用.

练习册系列答案
 导学与测试系列答案
导学与测试系列答案 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案
相关题目
 ,配方后得( )
,配方后得( )  B.
B.
 D.
D.
 , 则
, 则  ( )
( ) D.
D.

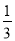 CE时,EP+BP= .
CE时,EP+BP= . 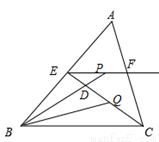
 的绝对值是( )
的绝对值是( ) B.
B. C.
C. D.2
D.2