题目内容
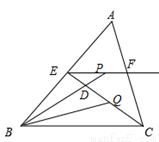
如图在△ABC中∠A=70°，⊙O截△ABC的三条边所得的弦长相等，则∠BOC的度数为（ ）
A．140° B．135° C．130° D．125°
D．
【解析】
试题分析：∵△ABC中∠A=70°，⊙O截△ABC的三条边所得的弦长相等，
∴O到三角形三条边的距离相等，即O是△ABC的内心，
∴∠1=∠2，∠3=∠4，∠1+∠3=
（180°-∠A）=（180°-70°）=55°，
∴∠BOC=180°-（∠1+∠3）=180°-55°=125°．
故选D．
考点：1.三角形的内切圆与内心；2.三角形内角和定理．
练习册系列答案
阅读快车系列答案
相关题目
，配方后得（ ） 
B.
D.
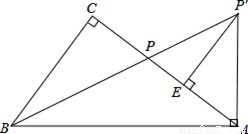
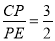，，BP′=5
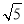时，求线段AB的长．
CE时，EP+BP= ． 
