题目内容
7.四边形ABCD中,AD=5$\sqrt{2}$,BC=6,连接AC,BD,AC⊥BC,BD⊥AD,∠DCA=45°.求AB的长及△DCB面积.分析 先作CE⊥BD交BD于点E,作AF⊥CD交CD的延长线于点F,由AC⊥BC,BD⊥AD,可得A、B、C、D四点共圆,进而得出∠ABD=∠DCA=45°,由AD=BD,可求出AB的值,利用勾股定理得出AC的值,利用RT△AFC可得CF的值,在RT△AFD中可得DF的值,由CD=CF-DF,可得CD的值,利用∠BAC=∠BDC,可得CE的值,由S△DCB=$\frac{1}{2}$BD•CE即可求出△DCB面积.
解答 解:如图,作CE⊥BD交BD于点E,作AF⊥CD交CD的延长线于点F,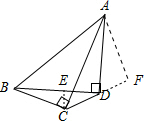
∵AC⊥BC,BD⊥AD,
∴∠ACB=∠ADB=90°,
∴A、B、C、D四点共圆,
∴∠ABD=∠DCA=45°,
∵AD=BD=5$\sqrt{2}$,
∴AB=$\sqrt{2}$AD=10,
∵BC=6,
∴AC=$\sqrt{A{B}^{2}-B{C}^{2}}$=$\sqrt{1{0}^{2}-{6}^{2}}$=8,
∵∠DCA=45°,∠AFC=90°,
∴CF=AF=4$\sqrt{2}$,
∵AD=5$\sqrt{2}$,
∴DF=$\sqrt{A{D}^{2}-A{F}^{2}}$=3$\sqrt{2}$,
∴CD=CF-DF=$\sqrt{2}$,
∵sin∠BAC=$\frac{BC}{AB}$=$\frac{3}{5}$,∠BAC=∠BDC,
∴$\frac{CE}{CD}$=$\frac{3}{5}$,即$\frac{CE}{\sqrt{2}}$=$\frac{3}{5}$,
解得CE=$\frac{3\sqrt{2}}{5}$,
∴S△DCB=$\frac{1}{2}$BD•CE=$\frac{1}{2}$×5$\sqrt{2}$×$\frac{3\sqrt{2}}{5}$=3.
点评 本题主要考查了四点共圆,涉及四点共圆的判定,勾股定理,直角三角形,正弦等知识,解题的关键是正确的作出辅助线,得出CD的值.

| A. | 42 | B. | -42 | C. | ±21 | D. | ±42 |

| A. | 8 | B. | 7 | C. | 6 | D. | 5 |
 如图,在长为10cm,宽为6cm的矩形中,截去一个矩形,使得留下的矩形(图中阴影部分)与原矩形相似,则留下的矩形面积是$\frac{108}{5}$cm2.
如图,在长为10cm,宽为6cm的矩形中,截去一个矩形,使得留下的矩形(图中阴影部分)与原矩形相似,则留下的矩形面积是$\frac{108}{5}$cm2.