题目内容
 如图,线段OC在数轴的正半轴上,O为原点,点C所表示的数是2,已知AB⊥BC,∠ACO=15°,OA=OC,则点B在数轴上表示的数是
如图,线段OC在数轴的正半轴上,O为原点,点C所表示的数是2,已知AB⊥BC,∠ACO=15°,OA=OC,则点B在数轴上表示的数是考点:实数与数轴,含30度角的直角三角形
专题:
分析:先由等腰三角形的性质及三角形外角的性质得出∠AOB=∠ACO+∠OAC=30°,然后利用含30度角的直角三角形的性质求出AB=
OA=1,根据勾股定理得到OB=
=
,再根据点B在原点的左侧,从而得出点B所表示的数.
| 1 |
| 2 |
| OA2-AB2 |
| 3 |
解答:解:∵OA=OC,
∴∠ACO=∠OAC=15°,
∴∠AOB=∠ACO+∠OAC=30°,
∵AB⊥BC,OA=2,
∴AB=
OA=1,OB=
=
=
,
∴点B在数轴上表示的数是-
.
故答案为-
.
∴∠ACO=∠OAC=15°,
∴∠AOB=∠ACO+∠OAC=30°,
∵AB⊥BC,OA=2,
∴AB=
| 1 |
| 2 |
| OA2-AB2 |
| 22-12 |
| 3 |
∴点B在数轴上表示的数是-
| 3 |
故答案为-
| 3 |
点评:本题考查了实数和数轴,等腰三角形的性质,三角形外角的性质,含30度角的直角三角形的性质以及勾股定理,难度适中.

练习册系列答案
 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案
相关题目
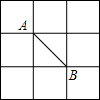 如图,A,B是3×3的正方形网格中的两个格点,C也是网格中的一个格点,连接AC、BC,当△ABC为等腰三角形时,格点C的不同位置有( )
如图,A,B是3×3的正方形网格中的两个格点,C也是网格中的一个格点,连接AC、BC,当△ABC为等腰三角形时,格点C的不同位置有( )| A、5个 | B、6个 | C、7个 | D、8个 |
在阳光下摆弄一个矩形,它的影子不可能是( )
| A、线段 | B、矩形 |
| C、等腰梯形 | D、平行四边形 |
上午8:30时,时钟的时针和分针所成的角度是( )
| A、75° | B、85° |
| C、70° | D、60° |
如果两个相似三角形的面积比是1:2,那么它们的周长比是( )
| A、1:4 | ||
B、1:
| ||
C、
| ||
| D、4:1 |
对于一次函数y=kx-k(k≠0),下列叙述正确的是( )
| A、当k>0时,函数图象经过第一、二、三象限 |
| B、当k>0时,y随x的增大而减小 |
| C、当k<0时,函数图象一定交于y轴负半轴一点 |
| D、函数图象一定经过点(1,0) |

 如图所示,已知线段AB=12cm,点O是AB上一点,C为AO的中点,点D在线段OB上,且AO:OD:DB=3:2:1,求线段AC的长.
如图所示,已知线段AB=12cm,点O是AB上一点,C为AO的中点,点D在线段OB上,且AO:OD:DB=3:2:1,求线段AC的长.