题目内容
如图,二次函数y=-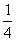 x2+bx+c的图像经过点A(4,0)B(-4,-4),且与y轴交于点C.
x2+bx+c的图像经过点A(4,0)B(-4,-4),且与y轴交于点C.
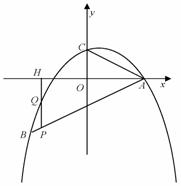
(1)求此二次函数的解析式;
(2)证明:∠BAO=∠CAO(其中O是原点);
(3)若P是线段AB上的一个动点(不与A、B重合),过P作y轴的平行线,分别交此二次函数图像及x轴于Q、H两点,试问:是否存在这样的点 P,使PH=2QH?若存在,请求出点P的坐标;若不存在,请说明理由.
(1)y=-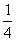 x2+
x2+ x+2;(2)证明见解析;(3)(-1,-
x+2;(2)证明见解析;(3)(-1,-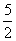 )与(-3,-
)与(-3,-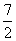 ).
).
【解析】(1)∵点A(4,0)与B(-4,-4)在二次函数图像上,
∴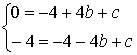 ,解得
,解得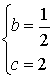 ,∴二次函数解析式为y=-
,∴二次函数解析式为y=-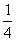 x2+
x2+ x+2.
x+2.
(2)过B作BD⊥x轴于点D,由(1)得C(0,2)
在Rt△AOC中,tan∠CAO=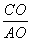 =
=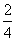 =
= ,
,
在Rt△ABD中,tan∠BAD=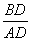 =
=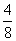 =
= ,
,
∵tan∠CAO= tan∠BAD ,∴∠CAO=∠BAD
(3)由A(4,0)与B(-4,-4),可得直线AB的解析式为y= x-2,
x-2,
设P(x, x-2),(
x-2),(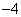 <
<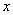 <4),则Q(x,-
<4),则Q(x,-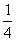 x2+
x2+ x+2),
x+2),
∴PH=| x-2|=2-
x-2|=2- x QH=|-
x QH=|-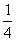 x2+
x2+ x+2|.
x+2|.
∴2- x =2|-
x =2|-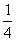 x2+
x2+ x+2|
x+2|
当2- x =-
x =- x2+x+4, 解得 x1=-1,x2=4(舍去),∴P(-1,-
x2+x+4, 解得 x1=-1,x2=4(舍去),∴P(-1,-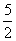 )
)
当2- x =
x = x2-x-4, 解得x1=-3,x2=4(舍去),∴P(-3,-
x2-x-4, 解得x1=-3,x2=4(舍去),∴P(-3,-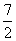 )
)
综上所述,存在满足条件的点,它们是(-1,-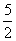 )与(-3,-
)与(-3,-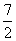 ).
).

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目


 6w=100.求x+y+z+w的最大值和最小值
6w=100.求x+y+z+w的最大值和最小值 .则新品种花生亩产量的增长率为
.则新品种花生亩产量的增长率为 8cm.点D、E、F分别是
8cm.点D、E、F分别是 边AB,BC,AC的中点,连接DE,DF,动点P,Q分别从点A、B同时出发,运动速度均为1cm/s,点P沿AFD的方向运动到点D停止;
边AB,BC,AC的中点,连接DE,DF,动点P,Q分别从点A、B同时出发,运动速度均为1cm/s,点P沿AFD的方向运动到点D停止; 点Q沿BC的方向运动,当点P停止运动时
点Q沿BC的方向运动,当点P停止运动时 也停止运动.在运动过程中,过点Q作BC的垂线交AB于点M,以点P,M,Q为顶点作平行四边形PMQN.设平行四边形边形PMQ
也停止运动.在运动过程中,过点Q作BC的垂线交AB于点M,以点P,M,Q为顶点作平行四边形PMQN.设平行四边形边形PMQ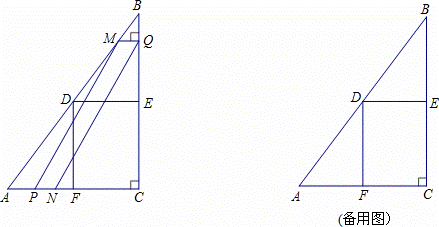
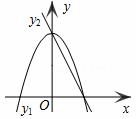
 2.若y1≠y2,取y1、y2中的较大值记为M;若y1=y2
2.若y1≠y2,取y1、y2中的较大值记为M;若y1=y2 ,记M=y1=y2。例如:当x=﹣1时,y1=0,y2=4,y1<y2,此时M=4。下列判断:
,记M=y1=y2。例如:当x=﹣1时,y1=0,y2=4,y1<y2,此时M=4。下列判断: x<0时,y1>y2;
x<0时,y1>y2; 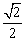 。
。