题目内容
如图,在平面直角坐标系中,坐标原点为O,A点坐标为(4,0),B点坐标为(﹣1,0),以AB的中点P为圆心,AB为直径作⊙P的正半轴交于点C.

(1)求经过A、B、C三点的抛物线所对应的函数解析式;
(2)设M为(1)中抛物线的顶点,求直线MC对应的函数解析式;
(3)试说明直线MC与⊙P的位置关系,并证明你的结论.
(1)y=-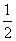 x2+
x2+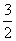 x+2,(2)
x+2,(2)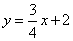 .(3)MC与⊙P的位置关系是相切.证明见解析.
.(3)MC与⊙P的位置关系是相切.证明见解析.
【解析】 (1)连接PC,
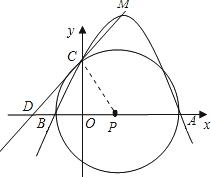
∵A(4,0),B(-1,0),∴AB=5,半径PC=PB=PA=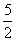 ,∴OP=
,∴OP=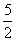 -1=
-1=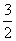 ,
,
在△CPO中,由勾股定理得:OC=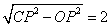 ,∴C(0,2),
,∴C(0,2),
设经过A、B、C三点抛物线解析式是y=a(x-4)(x+1),
把C(0,2)代入得:2=a(0-4)(0+1),∴a=-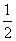 ,
,
∴y=-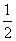 (x-4)(x+1)=-
(x-4)(x+1)=-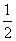 x2+
x2+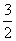 x+2,
x+2,
(2)y=-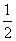 x2+
x2+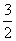 x+2=-
x+2=-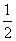 (x-
(x-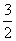 )2+
)2+ ,M(
,M(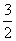 ,
, ),
),
设直线MC对应函数表达式是y=kx+b,把C(0,2),M(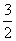 ,
, )代入得:
)代入得:
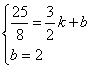 ,解得:
,解得: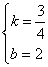 ,∴
,∴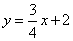 .
.
(3)MC与⊙P的位置关系是相切.
设直线MC交x轴于D,当y=0时,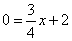 ,∴x=-
,∴x=-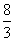 ,OD=
,OD=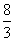 ,
,
∴D(-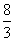 ,0),在△COD中,由勾股定理得:CD2=22+(
,0),在△COD中,由勾股定理得:CD2=22+(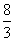 )2=
)2=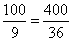 ,
,
PC2=(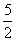 )2=
)2=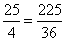 ,PD2=(
,PD2=(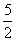 +
+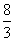 -1)2=
-1)2=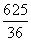 ,∴CD2+PC2=PD2,∴∠PCD=90°,
,∴CD2+PC2=PD2,∴∠PCD=90°,
∴PC⊥DC,∵PC为半径,∴MC与⊙P的位置关系是相切.

练习册系列答案
 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案
相关题目

 ,
, 是方程
是方程 的两个根,则
的两个根,则 的值为( )
的值为( ) 角(
角(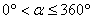 )得到
)得到 ,点P的对应点为
,点P的对应点为
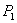 ,连
,连 ,在旋转过程中,线段
,在旋转过程中,线段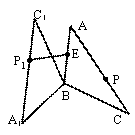
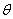 (0°<
(0°< 开始,用等长的小棒依次向右摆放,其中 A
开始,用等长的小棒依次向右摆放,其中 A 为第一根小棒,且 A
为第一根小棒,且 A
 的式子表示)
的式子表示)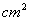 ),y随x变化的图象可能是( )
),y随x变化的图象可能是( )

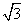 ,AF平分∠DAB,过C点作CE
,AF平分∠DAB,过C点作CE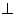 BD于E,延长AF、EC交于点H,下列结论中:①AF=FH;②B0=BF;③CA=CH;④BE=3ED;正确的个数为( )
BD于E,延长AF、EC交于点H,下列结论中:①AF=FH;②B0=BF;③CA=CH;④BE=3ED;正确的个数为( )
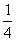 x2+bx+c的图像经过点A(4,0)B(-4,-4),且与y轴交于点C.
x2+bx+c的图像经过点A(4,0)B(-4,-4),且与y轴交于点C.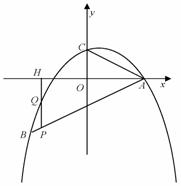

 的图
的图 象经过点P(3,-2),则当x<-3时,函数值
象经过点P(3,-2),则当x<-3时,函数值 的取值范围是【 】
的取值范围是【 】
 C.
C.