题目内容
 如图,在△ABC中,AD平分∠BAC,∠C=90°,DE⊥AB于E,BD=DF,求证:CF=EB.
如图,在△ABC中,AD平分∠BAC,∠C=90°,DE⊥AB于E,BD=DF,求证:CF=EB.考点:角平分线的性质,全等三角形的判定与性质
专题:证明题
分析:根据角平分线的性质“角平分线上的点到角的两边的距离相等”,可得点D到AB的距离=点D到AC的距离即DE=CD,再根据HL证明Rt△CDF≌Rt△EBD,从而得出CF=EB.
解答:证明:∵AD平分∠BAC,∠C=90°,DE⊥AB于E,
∴DE=DC.
在△CDF与△EDB中,
,
∴Rt△CDF≌Rt△EDB(HL),
∴CF=EB.
∴DE=DC.
在△CDF与△EDB中,
|
∴Rt△CDF≌Rt△EDB(HL),
∴CF=EB.
点评:本题主要考查角平分线的性质,全等三角形的判定与性质.求得CD=DE是解答本题的关键.

练习册系列答案
 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目

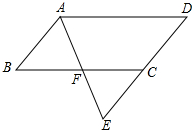 如图所示,将平行四边形ABCD的边DC延长到点E,使CE=DC,连接AE,交BC于点F,
如图所示,将平行四边形ABCD的边DC延长到点E,使CE=DC,连接AE,交BC于点F, 应用题:求如图所示的Rt△ABC的面积.
应用题:求如图所示的Rt△ABC的面积.