题目内容
11. 如图,OA、OB是⊙O的半径,C是⊙O上一点,∠ACB=20°,则∠OAB的度数为( )
如图,OA、OB是⊙O的半径,C是⊙O上一点,∠ACB=20°,则∠OAB的度数为( )| A. | 80° | B. | 75° | C. | 70° | D. | 65° |
分析 由OA、OB是⊙O的半径,C是⊙O上一点,∠ACB=20°,根据圆周角定理,可求得∠AOB的度数,然后由等腰三角形的性质,求得答案.
解答 解:∵∠ACB=20°,
∴∠AOB=2∠ACB=40°,
∵OA=OB,
∴∠OAB=∠OBA=70°.
故选C.
点评 此题考查了圆周角定理以及等腰三角形的性质.注意在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.

练习册系列答案
相关题目
17.下列命题中,错误的是( )
| A. | 两组对边分别平行的四边形是平行四边形 | |
| B. | 有一个角是直角的平行四边形是矩形 | |
| C. | 有一组邻边相等的平行四边形是菱形 | |
| D. | 内错角相等 |
18.计算(+5)+(-2)的结果是( )
| A. | 7 | B. | -7 | C. | 3 | D. | -3 |
16. 如图,A,B,C是⊙O上三个点,∠ACB=30°,则∠BAO的度数是( )
如图,A,B,C是⊙O上三个点,∠ACB=30°,则∠BAO的度数是( )
 如图,A,B,C是⊙O上三个点,∠ACB=30°,则∠BAO的度数是( )
如图,A,B,C是⊙O上三个点,∠ACB=30°,则∠BAO的度数是( )| A. | 55° | B. | 60° | C. | 65° | D. | 70° |
3.在直角坐标系中,直线a向上平移2个单位后所得直线b经过点A(0,3),直线b绕点A顺时针旋转90°后所得直线经过点B($\sqrt{3},0$),则直线a的解析式为( )
| A. | y=-$\sqrt{3}x+3$ | B. | y=-$\frac{\sqrt{3}}{3}x+1$ | C. | y=$\sqrt{3}x+1$ | D. | y=$\frac{\sqrt{3}}{3}x+1$ |
1. 已知点M、N、P、Q在数轴上的位置如图,则其中对应的数的绝对值最大的点是( )
已知点M、N、P、Q在数轴上的位置如图,则其中对应的数的绝对值最大的点是( )
 已知点M、N、P、Q在数轴上的位置如图,则其中对应的数的绝对值最大的点是( )
已知点M、N、P、Q在数轴上的位置如图,则其中对应的数的绝对值最大的点是( )| A. | M | B. | N | C. | P | D. | Q |

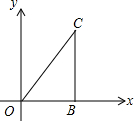 如图所示:在直角坐标系中,△OBC是直角三角形,OB与x轴正半轴重合,∠OBC=90°,且OB=1,BC=$\sqrt{3}$,将△OBC绕原点O逆时针旋转60°得到△OB1C1,将△OB1C1绕原点O逆时针旋转60°得到△OB2C2,…如此继续,得到△OB2016C2016则点C2016的坐标是(-2,0).
如图所示:在直角坐标系中,△OBC是直角三角形,OB与x轴正半轴重合,∠OBC=90°,且OB=1,BC=$\sqrt{3}$,将△OBC绕原点O逆时针旋转60°得到△OB1C1,将△OB1C1绕原点O逆时针旋转60°得到△OB2C2,…如此继续,得到△OB2016C2016则点C2016的坐标是(-2,0).