题目内容
18．若△+△=※，○=□+□，△=○+○+○+○，则※÷□等于（ ）| A． | 2 | B． | 4 | C． | 8 | D． | 16 |
分析 根据题中的三个等式，将原式化简即可得到结果．
解答 解：根据题意得：
※÷□=（△+△）÷□
=[（○+○+○+○）+（○+○+○+○）]÷□
=8○÷□
=8（□+□）÷□
=16□÷□
=16，
故选D
点评 此题考查了有理数的加法，熟练掌握运算法则是解本题的关键．
练习册系列答案
口算题卡加应用题集训系列答案
综合自测系列答案
相关题目
8．已知a，b均为实数，且a＞b，下列结论成立的是（ ）
| A． | a+2014＜b+2014 | B． | 2014a＜2014b | C． | $\frac{a}{2014}＜\frac{b}{2014}$ | D． | -2104a＜-2014b |
9．
如图，∠1=70°，∠2=70°，∠3=60°，则∠4的度数等于（ ）
如图，∠1=70°，∠2=70°，∠3=60°，则∠4的度数等于（ ）| A． | 80° | B． | 70° | C． | 60° | D． | 50° |
6．已知A=a2-a+4，B=3a-1，则A、B的大小关系为（ ）
| A． | A＞B | B． | A=B | C． | A＜B | D． | 不能确定 |
13．当a，b互为相反数时，代数式a2+ab-2的值为（ ）
| A． | 2 | B． | 0 | C． | -2 | D． | -1 |
3．
如图，在Rt△ABC中，∠ACB=90°，∠A=60°，过点C的直线与AB交于点D，且将△ABC的面积分成相等的两部分，则∠CDA=（ ）
如图，在Rt△ABC中，∠ACB=90°，∠A=60°，过点C的直线与AB交于点D，且将△ABC的面积分成相等的两部分，则∠CDA=（ ）| A． | 30° | B． | 45° | C． | 60° | D． | 75° |
10．
如图，在四边形ABCD中，AB=BC，∠ABC=∠CDA=90°，BE⊥AD于点E，如果四边形ABCD的面积为8，那么BE的长为（ ）
如图，在四边形ABCD中，AB=BC，∠ABC=∠CDA=90°，BE⊥AD于点E，如果四边形ABCD的面积为8，那么BE的长为（ ）| A． | 2 | B． | 3 | C． | 2$\sqrt{2}$ | D． | 2$\sqrt{3}$ |
将两块全等的三角板如图放置，点O为AB中点，AB=A′B′=10，BC=B′C′=6，现将三角板A′B′C′绕点O旋转，B′C′、A′B′与边AC分别交于点M、N，当CM=$\frac{25}{8}$或$\frac{7}{4}$时，△OMN与△BCO相似．
8．
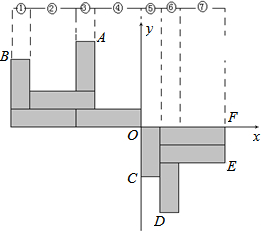用如图大小形状完全相同的长方形纸片在直角坐标系中摆成以下图案，已知A（-2，6）．
（1）求出长方形的长与宽；
（2）写出B、C、D、E、F点的坐标；
（3）要使点P（m，n）在长方形纸片拼成的图案阴影内（可以在边上），在下面的表中填写：m在哪一范围内取值时，n对应的范围是什么．
用如图大小形状完全相同的长方形纸片在直角坐标系中摆成以下图案，已知A（-2，6）．（1）求出长方形的长与宽；
（2）写出B、C、D、E、F点的坐标；
（3）要使点P（m，n）在长方形纸片拼成的图案阴影内（可以在边上），在下面的表中填写：m在哪一范围内取值时，n对应的范围是什么．
| 范围顺序号 | m的范围 | n对应的范围 |
| 1 | -2≤m≤0 | 0$≤n≤\frac{4}{3}$ |
| 2 | -$\frac{10}{3}$≤m＜-2 | 0≤n≤6 |
| 3 | -$\frac{16}{3}$≤m＜-$\frac{10}{3}$ | 0≤n≤$\frac{8}{3}$ |
| 4 | -$\frac{20}{3}$≤m＜-$\frac{16}{3}$ | 0$≤n≤\frac{14}{3}$ |
| 5 | 0＜m$≤\frac{4}{3}$ | -$\frac{10}{3}$≤n≤0 |
| 6 | $\frac{4}{3}$＜m≤$\frac{8}{3}$ | -6≤n≤0 |
| 7 | $\frac{8}{3}$＜m≤$\frac{14}{3}$ | 0≤n≤-$\frac{8}{3}$ |