题目内容

在实数的原有运算中，我们补充两种新运算，其中“1⊕n”表示从1到n连续正整数的和，即：1⊕n=1+2+3+…+（n-1）+n；“1?n”表示从1到n连续正整数的积，即：1?n=1×2×3×…×（n-1）×n．则（1⊕2009）-（1⊕2010）+

）的值为（）
A．-2010
B．-2009
C．0
D．2010

【答案】分析：根据新定义1⊕n=1+2+3+…+（n-1）+n，把（1⊕2009）-（1⊕2010）展开，然后再根据1?n=1×2×3×…×（n-1）×n，再把

展开，然后再计算即可．
解答：解：（1⊕2009）-（1⊕2010）+

）=（1+2+3+…+2009）-（1+2+3…+2010）+

=-2010+2010=0．
故选C．
点评：本题考查了实数的运算法则，解题的关键是正确的理解新定义并学会运用，此题比较繁琐，计算时要细心才行．

练习册系列答案

教材解读与拓展系列答案

在实数的原有运算中，我们补充两种新运算，其中“1⊕n”表示从1到n连续正整数的和，即：1⊕n=1+2+3+…+（n-1）+n；“1?n”表示从1到n连续正整数的积，即：1?n=1×2×3×…×（n-1）×n．则（1⊕2009）-（1⊕2010）+ $数学公式$ ）的值为

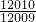在实数的原有运算中，我们补充两种新运算，其中“1⊕n”表示从1到n连续正整数的和，即：1⊕n=1+2+3+…+（n-1）+n；“1?n”表示从1到n连续正整数的积，即：1?n=1×2×3×…×（n-1）×n．则（1⊕2009）-（1⊕2010）+）的值为