题目内容
4.已知方程组$\left\{\begin{array}{l}{x+y=4-2k}\\{x-3y=2}\end{array}\right.$,k是整数.(1)若方程组的解x、y适合x=2y,求k的值;
(2)若方程组的解x、y满足x-y>0,求不等式组$\left\{\begin{array}{l}{2x+1<3x+3}\\{2x+1>x+2}\\{x-k≤0}\end{array}\right.$.
分析 (1)解方程组,求出方程组的解,根据x=2y列出方程,即可解答;
(2)由x-y>0,解得:k<3,方程组$\left\{\begin{array}{l}{2x+1<3x+3}\\{2x+1>x+2}\\{x-k≤0}\end{array}\right.$解得:$\left\{\begin{array}{l}{x>-2}\\{x>1}\\{x≤k}\end{array}\right.$因为k<3,所以不等式组的解集为:1<x≤k.
解答 解:(1)$\left\{\begin{array}{l}{x+y=4-2k}\\{x-3y=2}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{x=\frac{7-3k}{2}}\\{y=\frac{1-k}{2}}\end{array}\right.$,
∵x=2y,
∴$\frac{7-3k}{2}=2×\frac{1-k}{2}$,不等式组$\left\{\begin{array}{l}{2x+1<3x+3}\\{2x+1>x+2}\\{x-k≤0}\end{array}\right.$.
解得:k=5.
(2)∵x-y>0,
∴x>y,
∴$\frac{7-3k}{2}>\frac{1-k}{2}$,
解得:k<3,
$\left\{\begin{array}{l}{2x+1<3x+3}\\{2x+1>x+2}\\{x-k≤0}\end{array}\right.$
解得:$\left\{\begin{array}{l}{x>-2}\\{x>1}\\{x≤k}\end{array}\right.$
∵k<3,
∴不等式组的解集为:1<x≤k.
点评 本题考查了二元一次方程组的解,解决本题的关键是求出方程组的解,并根据已知条件列不等式.

 灵星计算小达人系列答案
灵星计算小达人系列答案 孟建平错题本系列答案
孟建平错题本系列答案| A. | $\sqrt{20}$ | B. | $\sqrt{19}$ | C. | $\sqrt{18}$ | D. | $\sqrt{\frac{1}{5}}$ |
 如图,在平面直角坐标系中,正方形ABCD的顶点A落在y轴上,点C落在x轴上,随着顶点C由原点O向x轴正半轴方向运动,顶点A沿y轴负半轴方向运动到终点O,在运动过程中OD的长度变化情况是( )
如图,在平面直角坐标系中,正方形ABCD的顶点A落在y轴上,点C落在x轴上,随着顶点C由原点O向x轴正半轴方向运动,顶点A沿y轴负半轴方向运动到终点O,在运动过程中OD的长度变化情况是( )| A. | 一直增大 | B. | 一直减小 | C. | 先减小后增大 | D. | 先增大后减少 |
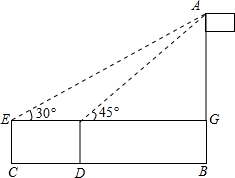 如图,身高1.6米的小明为了测量学校旗杆AB的高度,在平地上C处测得旗杆高度顶端A的仰角为30°,沿CB方向前进3米到达D处,在D处测得旗杆顶端A的仰角为45°,求旗杆AB的高度($\sqrt{3}=1.7,\sqrt{2}=1.4$)
如图,身高1.6米的小明为了测量学校旗杆AB的高度,在平地上C处测得旗杆高度顶端A的仰角为30°,沿CB方向前进3米到达D处,在D处测得旗杆顶端A的仰角为45°,求旗杆AB的高度($\sqrt{3}=1.7,\sqrt{2}=1.4$) 如图是一块正三角形花圃,为了分别种上红、黄、紫三种颜色的花,要求把它划分成三块面积相同的部分,并且使整个图形呈轴对称图形,请你至少设计三种不同方案.
如图是一块正三角形花圃,为了分别种上红、黄、紫三种颜色的花,要求把它划分成三块面积相同的部分,并且使整个图形呈轴对称图形,请你至少设计三种不同方案.