题目内容
有长为50厘米,宽为40厘米的长方形厚纸板三张,照以下甲,乙、丙三个图,在四角各截去不同规格的正方形后,再制成三个无盖纸盒,请问容积最大的纸盒是( )


| A、甲 | B、乙 | C、丙 | D、一样大 |
考点:展开图折叠成几何体,认识立体图形
专题:常规题型,计算题
分析:利用盒子体积公式底面积乘以高分别求出各纸盒的容积求出后比较即可.
解答:解:∵甲的容积为:(50-20)×(40-20)×10=6000(cm3),
乙的容积为:(50-8)×(40-8)×8=10752(cm3),
丙的容积为:(50-6)×(40-6)×6=8976(cm3),
∴容积最大的纸盒是乙.
故选:B.
乙的容积为:(50-8)×(40-8)×8=10752(cm3),
丙的容积为:(50-6)×(40-6)×6=8976(cm3),
∴容积最大的纸盒是乙.
故选:B.
点评:此题主要考查了展开图折叠成几何体以及立体图形体积求法,利用立方体体积公式求出是解题关键.

练习册系列答案
 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案
相关题目
若a<b,则下列各式正确的是( )
| A、3a>3b | ||||
| B、-3a>-3b | ||||
| C、a-3>b-3 | ||||
D、
|
 已知?ABCD的周长为32,AB=4,则BC=( )
已知?ABCD的周长为32,AB=4,则BC=( )| A、8 | B、12 | C、24 | D、28 |
已知三角形的三边的长依次为5,9,x,则x的取值范围是( )
| A、5<x<9 |
| B、4<x<9 |
| C、4<x<14 |
| D、5<x<14 |
平面直角坐标系中,点(1,-2)在( )
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
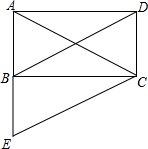 如图,在矩形ABCD中,将△ABD沿AB向下平移使A点到达B点,得到△BEC,下列说法正确的是( )
如图,在矩形ABCD中,将△ABD沿AB向下平移使A点到达B点,得到△BEC,下列说法正确的是( )| A、△ACE一定是等腰三角形 |
| B、△ACE一定是等边三角形 |
| C、△ACE一定是锐角三角形 |
| D、△ACE不可能是等腰直角三角形 |
 如图,P是⊙O的直径AB延长线上一点,PC切⊙O于C,∠P=50°,∠A为( )
如图,P是⊙O的直径AB延长线上一点,PC切⊙O于C,∠P=50°,∠A为( )| A、40° | B、35° |
| C、25° | D、20° |
 正方形网格中,每个小正方形的顶点称为格点,以格点为顶点的三角形叫格点三角形.在图中正方形网格(每个小正方形边长为1)中有一格点△ABC和一线段DE
正方形网格中,每个小正方形的顶点称为格点,以格点为顶点的三角形叫格点三角形.在图中正方形网格(每个小正方形边长为1)中有一格点△ABC和一线段DE