题目内容
 如图,MN为一段河流,A、B两村庄在以MN为直径的圆上,两村准备合资在河边P修一泵站(点P为动点)向两村输水.小明得到如下数据:⊙O的半径为2千米,A是半圆上的一个三等分点,B是
如图,MN为一段河流,A、B两村庄在以MN为直径的圆上,两村准备合资在河边P修一泵站(点P为动点)向两村输水.小明得到如下数据:⊙O的半径为2千米,A是半圆上的一个三等分点,B是 |
| AN |
考点:轴对称-最短路线问题,勾股定理,垂径定理
专题:
分析:作点B关于MN的对称点E,连接AE交MN于点P,和MN的交点P就是所求作的位置.根据题意先求出∠CAE,再根据勾股定理求出AE,即可得出PA+PB的最小值.
解答: 解:作点B关于MN的对称点E,连接AE交MN于点P
解:作点B关于MN的对称点E,连接AE交MN于点P
此时PA+PB最小,且等于AE.
作直径AC,连接CE,OE,
又∵B是
的中点,
∴
=
=
=
,
又∵A是半圆的三等份点,
∴∠AON=60°,∠NOE=
∠AON=30°,
∴∠AOE=90°,
∴∠CAE=45°,
又∵AC为圆的直径,
∴∠AEC=90°,
∴∠C=∠CAE=45°,
∴CE=AE=
AC=2
(千米),
即AP+BP的最小值是2
千米.
∵2
×5000=10000
(元);
∴两村购买水管的钱至少是10000
元.
 解:作点B关于MN的对称点E,连接AE交MN于点P
解:作点B关于MN的对称点E,连接AE交MN于点P此时PA+PB最小,且等于AE.
作直径AC,连接CE,OE,
又∵B是
 |
| AN |
∴
 |
| AB |
 |
| BN |
 |
| NE |
| 1 |
| 2 |
 |
| AN |
又∵A是半圆的三等份点,
∴∠AON=60°,∠NOE=
| 1 |
| 2 |
∴∠AOE=90°,
∴∠CAE=45°,
又∵AC为圆的直径,
∴∠AEC=90°,
∴∠C=∠CAE=45°,
∴CE=AE=
| ||
| 2 |
| 2 |
即AP+BP的最小值是2
| 2 |
∵2
| 2 |
| 2 |
∴两村购买水管的钱至少是10000
| 2 |
点评:本题考查了垂径定理及勾股定理的知识,此题的难点是确定点P的位置:找点B关于MN的对称点,再连接其中一点的对称点和另一点,和AE于MN的交点P就是所求作的位置.再根据弧的度数和圆心角的度数求出∠CAE,根据勾股定理求出AE即可.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案
相关题目
一直角三角形的斜边长比一直角边长大2,另一直角边长为6,则斜边长为( )
| A、4 | B、8 | C、10 | D、12 |
 如图,下列说法中错误的是( )
如图,下列说法中错误的是( )| A、∠3和∠5是同位角 |
| B、∠4和∠5是同旁内角 |
| C、∠2和∠4是对顶角 |
| D、∠1和∠4是内错角 |
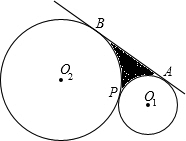 半径为1的O1与半径为3的O2外切于P点,如图所示,AB是两圆的外公切线,切点分别为点A、B,求AB和
半径为1的O1与半径为3的O2外切于P点,如图所示,AB是两圆的外公切线,切点分别为点A、B,求AB和 如图,矩形草坪的长是80m,宽是10m,现要修建一条平行于草坪边缘的矩形小路,使得小路矩形与草坪矩形相似,求小路的宽.
如图,矩形草坪的长是80m,宽是10m,现要修建一条平行于草坪边缘的矩形小路,使得小路矩形与草坪矩形相似,求小路的宽. 如图,已知△ABC中,M为BC的中点,AD是角平分线,MF⊥AD交AD的延长线于点F,交AB于点E,求证:BE=
如图,已知△ABC中,M为BC的中点,AD是角平分线,MF⊥AD交AD的延长线于点F,交AB于点E,求证:BE=