题目内容
一直角三角形的斜边长比一直角边长大2，另一直角边长为6，则斜边长为（ ）
| A、4 | B、8 | C、10 | D、12 |
考点：勾股定理
专题：
分析：设斜边长为x，则一直角边长为x-2，再根据勾股定理求出x的值即可．
解答：解：设斜边长为x，则一直角边长为x-2，
根据勾股定理得，62+（x-2）2=x2，
解得x=10，
故选C．
根据勾股定理得，62+（x-2）2=x2，
解得x=10，
故选C．
点评：本题考查的是勾股定理，熟知在任何一个直角三角形中，两条直角边长的平方之和一定等于斜边长的平方是解答此题的关键．
练习册系列答案
阅读快车系列答案
相关题目
下列各数是无理数的是（ ）
| A、7 | ||
B、
| ||
C、
| ||
D、
|
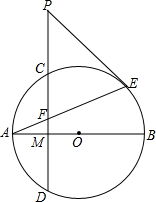如图，在⊙O中，直径AB与弦CD相交于点M，且M是CD的中点，点P在DC的延长线上，PE是⊙O的切线，E是切点，AE与CD相交于点F，PE与PF的大小有什么关系？为什么？
如图，MN为一段河流，A、B两村庄在以MN为直径的圆上，两村准备合资在河边P修一泵站（点P为动点）向两村输水．小明得到如下数据：⊙O的半径为2千米，A是半圆上的一个三等分点，B是