题目内容
如图，⊙O是△ABC的外接圆，AB=AC=10，BC=12，P是⊙O上的一个动点．
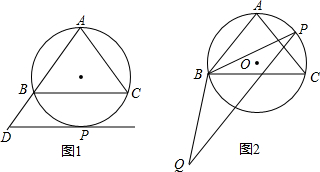
（1）若点P是弧
的中点，过点P作BC的平行线交AB的延长线于点D，求证：DP是⊙O的切线；
（2）若点P是弧
的中点，过点P作AB的平行线与射线BQ交于点Q，当BQ=BP时，求sin∠BQP的值．
（1）若点P是弧
 |
| BC |
（2）若点P是弧
|
| AC |
考点：切线的判定
专题：
分析：（1）根据点P是
的中点，得出
=
，得出PA是○O的直径，再利用DP∥BC，得出DP⊥PA，问题得证；
（2）先根据三角形的边长求得圆O的直径，再根据勾股定理求得OD、ED的长，进而求得AE的长，求得sin∠AEP=
=
，然后根据BQ=BP得出∠BQP=∠BPQ，根据AB∥PQ，得出∠APB=∠BPQ，因为∠AEP=∠ABP，从而得出∠BQP=∠AEP，即可求得sin∠BQP=sin∠AEP=
=
．
|
| BC |
|
| PBA |
|
| PCA |
（2）先根据三角形的边长求得圆O的直径，再根据勾股定理求得OD、ED的长，进而求得AE的长，求得sin∠AEP=
| AD |
| AE |
| ||
| 5 |
| AD |
| AE |
| ||
| 5 |
解答：
解：（1）连接AP，
∵AB=AC，
∴
=
，
又∵
=
，
∴
=
，
∴PA是⊙O的直径，
∵
=
，
∴∠1=∠2，
又AB=AC，
∴PA⊥BC，
又∵DP∥BC，
∴DP⊥PA，
∴DP是⊙O的切线．
（2）连接PO并延长交⊙O于E，做AF⊥BC垂足为G，连接CF，
∵AB=AC，
∴AF平分BC，
∴AF是⊙O的直径，
∵BG=CG=6，AC=10，
∴AG=
=8，
∵AC2=AG•AF，
∴AF=
，
∴EP=AF=
，OE=OA=
，
∴OD=
=
，
∴ED=OE+OD=10，
∴AE=
=5
，
∴sin∠AEP=
=
=
，
∵BQ=BP，
∴∠BQP=∠BPQ，
∵AB∥PQ，
∴∠ABP=∠BPQ，
∵∠AEP=∠ABP，
∴∠BQP=∠AEP，
∴sin∠BQP=sin∠AEP=
=
，
解：（1）连接AP，∵AB=AC，
∴
|
| AB |
|
| AC |
又∵
|
| PB |
|
| PC |
∴
|
| PBA |
|
| PCA |
∴PA是⊙O的直径，
∵
|
| PB |
|
| PC |
∴∠1=∠2，
又AB=AC，
∴PA⊥BC，
又∵DP∥BC，
∴DP⊥PA，
∴DP是⊙O的切线．
（2）连接PO并延长交⊙O于E，做AF⊥BC垂足为G，连接CF，
∵AB=AC，
∴AF平分BC，
∴AF是⊙O的直径，
∵BG=CG=6，AC=10，
∴AG=
| AC2-CG2 |
∵AC2=AG•AF，
∴AF=
| 25 |
| 2 |
∴EP=AF=
| 25 |
| 2 |
| 25 |
| 4 |
∴OD=
| OA2-AD2 |
| 15 |
| 4 |
∴ED=OE+OD=10，
∴AE=
| ED2+AD2 |
| 5 |
∴sin∠AEP=
| AD |
| AE |
| 5 | ||
5
|
| ||
| 5 |
∵BQ=BP，
∴∠BQP=∠BPQ，
∵AB∥PQ，
∴∠ABP=∠BPQ，
∵∠AEP=∠ABP，
∴∠BQP=∠AEP，
∴sin∠BQP=sin∠AEP=
| AD |
| AE |
| ||
| 5 |
点评：此题主要考查了切线的判定与性质以、勾股定理和圆周角定理以及平行线的性质，根据平行线的性质、圆周角的性质得出相等的角是解题关键．
练习册系列答案
相关题目
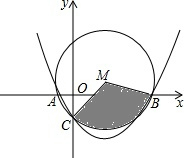已知抛物线y=ax2+bx-1，经过点A（-1，0），B（m，0）（m＞0），且与y轴交于点C．