题目内容
计算
（1）-20+（-14）-（-18）-13
（2）（-2）2×5-（-2）3+4
（3）2（2b+3a）-3（2a-3b）
（4）a2b-[2（a2b-2a2c）-（2bc+a2c）]．
（1）-20+（-14）-（-18）-13
（2）（-2）2×5-（-2）3+4
（3）2（2b+3a）-3（2a-3b）
（4）a2b-[2（a2b-2a2c）-（2bc+a2c）]．
考点：整式的加减,有理数的混合运算
专题：计算题
分析：（1）原式利用减法法则变形，计算即可得到结果；
（2）原式先计算乘方运算，再计算乘法运算，最后算加减运算即可得到结果；
（3）原式去括号合并即可得到结果；
（4）原式去括号合并即可得到结果．
（2）原式先计算乘方运算，再计算乘法运算，最后算加减运算即可得到结果；
（3）原式去括号合并即可得到结果；
（4）原式去括号合并即可得到结果．
解答：解：（1）原式=-20-14+18-13=-47+18=-29；
（2）原式=20+8+4=32；
（3）原式=4b+6a-6a+9b=13b；
（4）原式=a2b-2a2b+4a2c+2bc+a2c=-a2b+5a2c+2bc．
（2）原式=20+8+4=32；
（3）原式=4b+6a-6a+9b=13b；
（4）原式=a2b-2a2b+4a2c+2bc+a2c=-a2b+5a2c+2bc．
点评：此题考查了整式的加减，熟练掌握运算法则是解本题的关键．
练习册系列答案
相关题目
一次函数y=kx+|k-2|的图象过点（0，3），且y随x的增大而减小，则k的值为（ ）
| A、-1 | B、5 | C、5或-1 | D、-5 |
对于代数式x2-4x+6的值的情况，小明作了如下探究的结论，其中错误的是（ ）
| A、只有当x=2时，x2-4x+6的值为2 |
| B、x取大于2的实数时，x2-4x+6的值随x的增大而增大，没有最大值 |
| C、x2-4x+6的值随x的变化而变化，但是有最小值 |
| D、可以找到一个实数x，使x2-4x+6的值为0 |
小明不慎将一块三角形的玻璃打碎成如图所示的四块（图中所标1、2、3、4），你认为将其中的哪一块带去，就能配一块与原来大小一样的三角形玻璃？应该带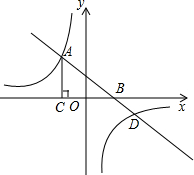
如图，在平面直角坐标系xOy中，一次函数y=kx+b与反比例函数y=