题目内容
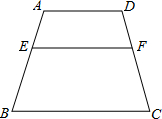 如图,已知:在梯形ABCD中,AD∥BC,AD=3,BC=5,点E在AB上,且AE:EB=2:3,过点E作EF∥BC交CD于F,则EF的长是________.
如图,已知:在梯形ABCD中,AD∥BC,AD=3,BC=5,点E在AB上,且AE:EB=2:3,过点E作EF∥BC交CD于F,则EF的长是________.
2.8
分析:首先过点A作AN∥CD,分别交EF,BC于点M,N,易得四边形AMFD与四边形ANCD是平行四边形,则可求得FM=CN=AD=3,BN=2,易证得△AEM∽△ABN,然后由相似三角形的对应边成比例,可求得EM的长,继而求得答案.
解答: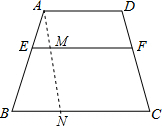 解:过点A作AN∥CD,分别交EF,BC于点M,N,
解:过点A作AN∥CD,分别交EF,BC于点M,N,
∵AD∥BC,EF∥BC,
∴AD∥EF∥BC,
∴四边形AMFD与四边形ANCD是平行四边形,
∴CN=MF=AD=3,
∴BN=BC-CN=5-3=2,
∵EF∥BC,
∴△AEM∽△ABN,
∴EN:BM=AE:AB,
∵AE:EB=2:3,
∴AE:AB=2:5,
∴EM= BN=0.8,
BN=0.8,
∴EF=AM+FM=2.8.
故答案为:2.8.
点评:此题考查了相似三角形的判定与性质、梯形的性质以及平行四边形的判定与性质.此题难度适中,注意掌握辅助线的作法,注意数形结合思想的应用.
分析:首先过点A作AN∥CD,分别交EF,BC于点M,N,易得四边形AMFD与四边形ANCD是平行四边形,则可求得FM=CN=AD=3,BN=2,易证得△AEM∽△ABN,然后由相似三角形的对应边成比例,可求得EM的长,继而求得答案.
解答:
 解:过点A作AN∥CD,分别交EF,BC于点M,N,
解:过点A作AN∥CD,分别交EF,BC于点M,N,∵AD∥BC,EF∥BC,
∴AD∥EF∥BC,
∴四边形AMFD与四边形ANCD是平行四边形,
∴CN=MF=AD=3,
∴BN=BC-CN=5-3=2,
∵EF∥BC,
∴△AEM∽△ABN,
∴EN:BM=AE:AB,
∵AE:EB=2:3,
∴AE:AB=2:5,
∴EM=
 BN=0.8,
BN=0.8,∴EF=AM+FM=2.8.
故答案为:2.8.
点评:此题考查了相似三角形的判定与性质、梯形的性质以及平行四边形的判定与性质.此题难度适中,注意掌握辅助线的作法,注意数形结合思想的应用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
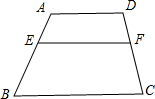 如图,已知:在梯形ABCD中,AD∥BC,AD=3,BC=5,点E在AB上,且AE:EB=2:3,过点E作EF∥BC交CD于F,求EF的长?
如图,已知:在梯形ABCD中,AD∥BC,AD=3,BC=5,点E在AB上,且AE:EB=2:3,过点E作EF∥BC交CD于F,求EF的长? 如图,已知:在梯形ABCD中,AD∥BC,AD=3,BC=5,点E在AB上,且AE:EB=2:3,过点E作EF∥BC交CD于F,则EF的长是
如图,已知:在梯形ABCD中,AD∥BC,AD=3,BC=5,点E在AB上,且AE:EB=2:3,过点E作EF∥BC交CD于F,则EF的长是 如图,已知:在梯形ABCD中,AD∥BC,AD=3,BC=5,点E在AB上,且AE:EB=2:3,过点E作EF∥BC交CD于F,求EF的长?
如图,已知:在梯形ABCD中,AD∥BC,AD=3,BC=5,点E在AB上,且AE:EB=2:3,过点E作EF∥BC交CD于F,求EF的长?
