题目内容
如图,已知:在梯形ABCD中,AD∥BC,AD=3,BC=5,点E在AB上,且AE:EB=2:3,过点E作EF∥BC交CD于F,求EF的长?
【答案】分析:首先过A作CD的平行线分别交EF于G,BC于H,由AE:EB=2:3,即可求得 ,然后由在梯形ABCD中,AD∥BC,AD=3,BC=5,根据平行线分线段成比例定理,即可求得EF的长.
,然后由在梯形ABCD中,AD∥BC,AD=3,BC=5,根据平行线分线段成比例定理,即可求得EF的长.
解答: 解:过A作CD的平行线分别交EF于G,BC于H,(1分)
解:过A作CD的平行线分别交EF于G,BC于H,(1分)
∵ ,
,
∴ ,(2分)
,(2分)
又∵EF∥BCAD∥BC,AD=3,BC=5,
∴GF=HC=AD=3,(1分)
∴BH=2,(1分)
 ,(2分)
,(2分)
∴EG= ,(1分)
,(1分)
∴EF=EG+GF=3+ =
= .(2分)
.(2分)
点评:此题考查了平行线分线段成比例定理.解题的关键是注意辅助线的作法与数形结合思想的应用.
 ,然后由在梯形ABCD中,AD∥BC,AD=3,BC=5,根据平行线分线段成比例定理,即可求得EF的长.
,然后由在梯形ABCD中,AD∥BC,AD=3,BC=5,根据平行线分线段成比例定理,即可求得EF的长.解答:
 解:过A作CD的平行线分别交EF于G,BC于H,(1分)
解:过A作CD的平行线分别交EF于G,BC于H,(1分)∵
 ,
,∴
 ,(2分)
,(2分)又∵EF∥BCAD∥BC,AD=3,BC=5,
∴GF=HC=AD=3,(1分)
∴BH=2,(1分)
 ,(2分)
,(2分)∴EG=
 ,(1分)
,(1分)∴EF=EG+GF=3+
 =
= .(2分)
.(2分)点评:此题考查了平行线分线段成比例定理.解题的关键是注意辅助线的作法与数形结合思想的应用.

练习册系列答案
 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目
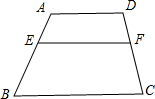 如图,已知:在梯形ABCD中,AD∥BC,AD=3,BC=5,点E在AB上,且AE:EB=2:3,过点E作EF∥BC交CD于F,求EF的长?
如图,已知:在梯形ABCD中,AD∥BC,AD=3,BC=5,点E在AB上,且AE:EB=2:3,过点E作EF∥BC交CD于F,求EF的长? 如图,已知:在梯形ABCD中,AD∥BC,AD=3,BC=5,点E在AB上,且AE:EB=2:3,过点E作EF∥BC交CD于F,则EF的长是
如图,已知:在梯形ABCD中,AD∥BC,AD=3,BC=5,点E在AB上,且AE:EB=2:3,过点E作EF∥BC交CD于F,则EF的长是 如图,已知:在梯形ABCD中,AD∥BC,AD=3,BC=5,点E在AB上,且AE:EB=2:3,过点E作EF∥BC交CD于F,求EF的长?
如图,已知:在梯形ABCD中,AD∥BC,AD=3,BC=5,点E在AB上,且AE:EB=2:3,过点E作EF∥BC交CD于F,求EF的长?