题目内容
如图,△ABC中,DE垂直平分AC,与AC交于E,与BC交于D,∠C=15°,∠BAD=60°,则△ABC是__________三角形.

直角三角形.
【考点】线段垂直平分线的性质 .
.
【专题】推理填空题.
【分析】根据线段垂直平分线的性质,可得AD=CD,则∠C=∠DAC=15°,所以,∠BAD+∠DAC+∠C=90°,即∠B=90°,即可得出;
【解答】解:∵DE垂直平分AC,
∴AD=CD,又∠C=15°,
∴∠C=∠DAC=15°,∠ADB=∠C+∠DAC=30°,
又∠BAD= 60°,
60°,
∴∠BAD+∠ADB=90°,
∴∠B=90°;
即△ABC是直角三角形;
故答案为:直角.

【点评】本题主要考查了线段垂直平分线的性质和直角三角形的判定,知道线段垂直平分线上的点到线段两个端点的距离相等.

练习册系列答案
 小学期末标准试卷系列答案
小学期末标准试卷系列答案
相关题目


 .16 B.18 C.26 D.28
.16 B.18 C.26 D.28 方形ABCD四边运动,求经过多长时间点P与点Q第一次在正方形ABCD边上的何处相遇?
方形ABCD四边运动,求经过多长时间点P与点Q第一次在正方形ABCD边上的何处相遇?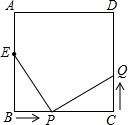

 的值为0.
的值为0.