Question

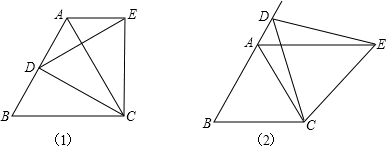
．如图，AD是△ABC的角平分线，DE⊥AC，垂足为E，BF∥AC交ED的延长线于点F，若BC恰好平分∠ABF，AE=2BF．给出下列四个结论：①DE=DF；②DB=DC；③AD⊥BC；④AC=3BF，其中正确的结论共有(     )

A．4个  B．3个   C．2个  D．1个

Answer 1

A【考点】全等三角形的判定与性质；角平分线的性质；相似三角形的判定与性质．

【分析】根据等腰三角形的性质三线合一得到BD=CD，AD⊥BC，故②③正确；通过△CDE≌△DBF，得到DE=DF，CE=BF，故①④正确．

【解答】解：∵BF∥AC，

∴∠C=∠CBF，

∵BC平分∠ABF，

∴∠ABC=∠CBF，

∴∠C=∠ABC，

∴AB=AC，

∵AD是△ABC的角平分线，

∴BD=CD，AD⊥BC，故②③正确，

在△CDE与△DBF中，

，

∴△CDE≌△DBF，

∴DE=DF，CE=BF，故①正确；

∵AE=2BF，

∴AC=3BF，故④正确．

故选A．

【点评】本题考查了全等三角形的判定和性质，等腰三角形的性质，平行线的性质，掌握等腰三角形的性质三线合一是解题的关键．