题目内容
19.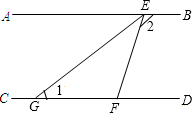 如图,AB∥CD,直线EF分别交AB、CD点E、F,EG平分∠AEF,
如图,AB∥CD,直线EF分别交AB、CD点E、F,EG平分∠AEF,(1)求证:△EGF是等腰三角形.
(2)若∠1=40°,求∠2的度数.
分析 (1)根据平行线的性质求出∠1=∠AEG,求出∠AEG=∠FEG,推出∠1=∠FEG,根据等腰三角形的判定推出即可;
(2)求出∠AEF的度数,根据邻补角定义求出即可.
解答 (1)证明:∵AB∥CD,
∴∠1=∠AEG,
∵EG平分∠AEF,
∴∠AEG=∠FEG,
∴∠1=∠FEG,
∴FE=FG,
即△EGF是等腰三角形;
(2)解:∵∠1=40°,∠1=∠AEG=∠FEG,
∴∠AEF=40°+40°=80°,
∴∠2=180°-80°=100°.
点评 本题考查了等腰三角形的判定,平行线的性质,角平分线的定义的应用,能求出∠1=∠AEG=∠FEG是解此题的关键,注意:两直线平行,内错角相等.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
7.将一张面值50元的人民币,兑换成5元或10元的零钱,那么兑换方案共有( )
| A. | 5种 | B. | 6种 | C. | 7种 | D. | 8种 |
14.在代数式$\frac{1}{2}$a+bac,$\frac{3b}{5}$,π,3x2-4x-2,$\frac{x+y}{xy}$,πab,0,$\frac{b}{a}$中,下列结论正确的是( )
| A. | 有4个单项式,2个多项式 | B. | 有4个单项式,3个多项式 | ||
| C. | 有7个整式 | D. | 有3个单项式,2个多项式 |
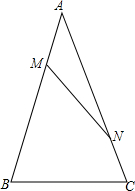 如图,已知△ABC中,AB=AC,AM=CN,探求:∠ABC与∠ANM满足∠B-∠ANM=30°时,$\frac{MN}{BC}$=$\frac{\sqrt{3}}{3}$.
如图,已知△ABC中,AB=AC,AM=CN,探求:∠ABC与∠ANM满足∠B-∠ANM=30°时,$\frac{MN}{BC}$=$\frac{\sqrt{3}}{3}$. 如图,矩形PMON的边OM,ON分别在坐标轴上,且点P的坐标为(-2,3).将矩形PMON绕点0顺时针旋转90°得到矩形P′M′O′M′
如图,矩形PMON的边OM,ON分别在坐标轴上,且点P的坐标为(-2,3).将矩形PMON绕点0顺时针旋转90°得到矩形P′M′O′M′