题目内容
9. 如图,矩形PMON的边OM,ON分别在坐标轴上,且点P的坐标为(-2,3).将矩形PMON绕点0顺时针旋转90°得到矩形P′M′O′M′
如图,矩形PMON的边OM,ON分别在坐标轴上,且点P的坐标为(-2,3).将矩形PMON绕点0顺时针旋转90°得到矩形P′M′O′M′(1)请画出旋转后的图形
(2)求直线OP的函数解析式.
分析 (1)根据旋转的定义先确定N的对应点N′和M的对应点M′,再利用四边形P′M′O′M′为矩形确定P的对应点P′;
(2)利用待定系数法求直线OP的解析式.
解答 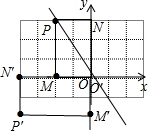 解:(1)如图:
解:(1)如图:
(2)设直线OP的解析式为y=kx,
把P(-2,3)代入得-2k=3,解得k=-$\frac{3}{2}$,
所以直线OP的解析式为y=-$\frac{3}{2}$x.
点评 本题考查了作图:旋转变换:根据旋转的性质可知,对应角都相等都等于旋转角,对应线段也相等,由此可以通过作相等的角,在角的边上截取相等的线段的方法,找到对应点,顺次连接得出旋转后的图形.也考查了待定系数法求一次函数解析式.

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
4.下列图形都是由同样大小的棋子按一定的规律组成,其中第①个图形有3颗棋子,第②个图形一共有9颗棋子,第③个图形一共有l8颗棋子,…,则第⑥个图形中棋子的颗数为( )
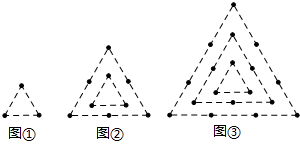

| A. | 63 | B. | 84 | C. | 108 | D. | 152 |
14.将某图形的横坐标都减去3,纵坐标不变,则该图形( )
| A. | 向左平移3个单位 | B. | 向右平移3个单位 | C. | 向上平移3个单位 | D. | 向下平移3个单位 |
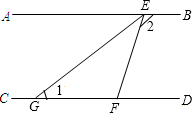 如图,AB∥CD,直线EF分别交AB、CD点E、F,EG平分∠AEF,
如图,AB∥CD,直线EF分别交AB、CD点E、F,EG平分∠AEF,