题目内容
已知x，y为任意有理数，记M=x2+y2，N=2xy，则M与N的大小关系为（ ）
| A、M＞N | B、M≥N |
| C、M≤N | D、不能确定 |
考点：因式分解-运用公式法,非负数的性质：偶次方
专题：
分析：首先求出M-N=x2+y2-2xy=（x-y）2，进而判断M与N的大小关系．
解答：解：∵M=x2+y2，N=2xy，
∴M-N=x2+y2-2xy=（x-y）2，
∵（x-y）2≥0，
∴M≥N．
故选：B．
∴M-N=x2+y2-2xy=（x-y）2，
∵（x-y）2≥0，
∴M≥N．
故选：B．
点评：此题主要考查了完全平方公式的应用以及偶次方的性质，得出M-N=（x-y）2是解题关键．
练习册系列答案
99加1领先期末特训卷系列答案
百强名校期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案
金状元绩优好卷系列答案
相关题目
如果tanα=0.213，那么锐角α的度数大约为（ ）
| A、8° | B、10° | C、12° |
由四舍五入得到的近似数是3.75，下面数字中不可能的是其真值的是（ ）
| A、3.7524 |
| B、3.7493 |
| C、3.7504 |
| D、3.7554 |
如图，AB=AC=12，BC=7，∠A=40°，AB的垂直平分线交AB于点交于点D，交AC于点E，△BCE的周长是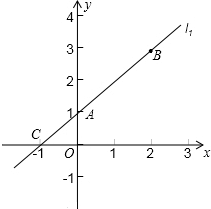
如图，已知直线l1经过点A（0，1）与点B（2，3），另一条直线l2经过点B，且与x轴相交于点P（m，0）．