题目内容
7.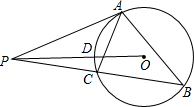 如图,PA是⊙O的切线,A是切点,B是圆上异于A的另一点,PB交⊙O于C,连接AB、AC.
如图,PA是⊙O的切线,A是切点,B是圆上异于A的另一点,PB交⊙O于C,连接AB、AC.(1)证明:PA2=PB•PC;
(2)若PB=4,C是PB的中点,圆的半径为y,点P和圆上一点连线的最小距离为x,求y关于x的函数解析式及x的取值范围.
分析 (1)作直径AE,连结CE,如图,根据切线的性质得∠EAC+∠CAP=90°,再根据圆周角定理得∠ACE=90°,所以∠E+∠EAC=90°,则∠E=∠CAP,加上∠E=∠B,则∠CAP=∠B,于是可判断△PAC∽△PBA,利用相似比和比例的性质可得PA2=PB•PC;
(2)由(1)的结论可得PA2=4×2=8,作直线OP交⊙O于D、F,则PD=x,DF=2y,与(1)同样方法可得到PA2=PD•PF,则x•(x+2y)=8,所以y=$\frac{8-{x}^{2}}{2x}$(0<x≤2,当BC为直径时,x最大).
解答 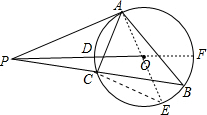 (1)证明:作直径AE,连结CE,如图,
(1)证明:作直径AE,连结CE,如图,
∵PA是⊙O的切线,
∴OA⊥PA,
∴∠OAP=90°,即∠EAC+∠CAP=90°,
∵AE为直径,
∴∠ACE=90°,
∴∠E+∠EAC=90°,
∴∠E=∠CAP,
∵∠E=∠B,
∴∠CAP=∠B,
而∠CPA=∠APB,
∴△PAC∽△PBA,
∴PA:PB=PC:PA,
∴PA2=PB•PC;
(2)解:∵PB=4,C是PB的中点,
∴PC=2,
∴PA2=4×2=8,
作直线OP交⊙O于D、F,则PD=x,DF=2y,
与(1)同样方法可得到PA2=PD•PF,
∴x•(x+2y)=8,
∴y=$\frac{8-{x}^{2}}{2x}$(0<x≤2,当BC为直径时,x最大).
点评 本题考查了切线的性质:圆的切线垂直于经过切点的半径.运用切线的性质来进行计算或论证,常通过作辅助线连接圆心和切点,利用垂直构造直角三角形解决有关问题.也考查了相似三角形的判定与性质.

练习册系列答案
相关题目
19.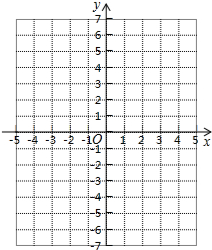 已知动点(x,y)的横纵坐标满足方程2y-x=2.
已知动点(x,y)的横纵坐标满足方程2y-x=2.
(1)请在表格中求出相应的x(或y)的值,并在图中平面直角坐标系中描出这些点:
(2)若将这五个点先向右平移5个单位长度,再向上平移3个单位长度,得到点A1,B1,C1,D1,E1,并分别写出它们的坐标.
 已知动点(x,y)的横纵坐标满足方程2y-x=2.
已知动点(x,y)的横纵坐标满足方程2y-x=2.(1)请在表格中求出相应的x(或y)的值,并在图中平面直角坐标系中描出这些点:
| 点的名称 | A | B | C | D | E |
| 点的横坐标x | -2 | 2 | |||
| 点的纵坐标y | -1 | 1 | 3 |
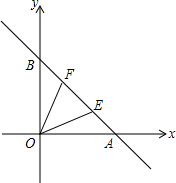 如图,直线y=-x+1与两坐标轴分别交于A、B两点,E、F为线段AB上的两个动
如图,直线y=-x+1与两坐标轴分别交于A、B两点,E、F为线段AB上的两个动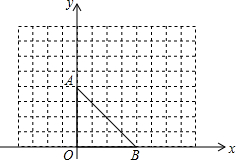 如图,点A的坐标是(0,4),点B的坐标是(4,0).
如图,点A的坐标是(0,4),点B的坐标是(4,0).