题目内容
15. 如图,在?ABCD的边AD上截取DE=DC,若∠ECB=65°,则∠A的度数是130°.
如图,在?ABCD的边AD上截取DE=DC,若∠ECB=65°,则∠A的度数是130°.
分析 根据等腰三角形的性质、平行四边形的性质以及平行线的性质得到∠DEC=∠DCE=∠ECB=65°,再结合平行四边形的对角相等进行计算.
解答 解:∵DE=DC,
∴∠DEC=∠DCE.
∵四边形ABCD是平行四边形,
∴AD∥BC,∠A=∠BCD.
∴∠DEC=∠ECB=65°,
∴∠DCE=∠ECB=65°,
∴∠BCD=∠ECB+∠DCE=130°,
∴∠A=130°.
故答案是:130°.
点评 本题主要考查平行四边形的性质,等腰三角形的性质以及平行线的性质.解答该题时,也可以利用三角形内角和定理和“两直线平行,同旁内角互补”进行答题.

练习册系列答案
相关题目
6.在Rt△ABC中,CD是斜边AB边的中线,若AB=8,则CD的长是( )
| A. | 6 | B. | 5 | C. | 4 | D. | 3 |
20.不等式2x+5>3的解集在数轴上表示正确的是( )
| A. |  | B. |  | C. |  | D. |  |
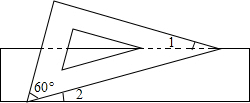 如图,有一块含有60°角的直角三角板的两个顶点放在矩形的对边上.如果∠1=15°,那么∠2的度数是15°.
如图,有一块含有60°角的直角三角板的两个顶点放在矩形的对边上.如果∠1=15°,那么∠2的度数是15°. 先阅读然后回答问题:
先阅读然后回答问题:



 实数a、b在数轴上的对应点如图所示,化简$\sqrt{(a-b)^{2}}$+|a+b|+$\sqrt{{b}^{2}}$=-3b.
实数a、b在数轴上的对应点如图所示,化简$\sqrt{(a-b)^{2}}$+|a+b|+$\sqrt{{b}^{2}}$=-3b.