题目内容
18.已知点M(0,1),N是抛物线y=x2-1上的一个动点,设MN=d,则d的最小值为$\frac{\sqrt{7}}{2}$.分析 设N(x,x2-1),作NA⊥y轴于A,则OA=x2-1,AN=x,MA=OM-OA=2-x2,由勾股定理和二次函数的最值得出d2的最小值=$\frac{7}{4}$,得出d有最小值为$\frac{\sqrt{7}}{2}$即可.
解答 解: 设N(x,x2-1),
设N(x,x2-1),
作NA⊥y轴于A,如图所示:
则OA=x2-1,AN=x,
∴MA=OM-OA=2-x2,
由勾股定理得:d2=MN2=MA2+AN2=(2-x2)2+x2=x4-3x2+4=(x2-$\frac{3}{2}$)2+$\frac{7}{4}$,
当x2=$\frac{3}{2}$时,d2的最小值=$\frac{7}{4}$,
∴d的最小值为$\frac{\sqrt{7}}{2}$.
故答案为:$\frac{\sqrt{7}}{2}$.
点评 本题考查了二次函数图象上点的坐标特征、二次函数的最值;熟练掌握二次函数图象上点的坐标特征是解决问题的关键.

练习册系列答案
相关题目
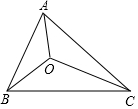 如图,△ABC的三边AB,CA,BC的长分别为40,50,60,其三条角平分线交与点O,则S△ABO:S△BCO:S△CAO=4:6:5.
如图,△ABC的三边AB,CA,BC的长分别为40,50,60,其三条角平分线交与点O,则S△ABO:S△BCO:S△CAO=4:6:5.