题目内容
20.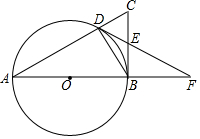 如图,AB是⊙O的直径,点D是⊙O上的一点,连接AD,BD.过点B作⊙O的切线BC交AD的延长线于点C,E为BC的中点,连接DE并延长交AB的延长线于点F.
如图,AB是⊙O的直径,点D是⊙O上的一点,连接AD,BD.过点B作⊙O的切线BC交AD的延长线于点C,E为BC的中点,连接DE并延长交AB的延长线于点F.(1)求证:DF为⊙O的切线;
(2)若EF=2DE=4,求⊙O的半径.
分析 (1)连接OD,由AB为⊙O的直径得∠BDC=90°,根据BE=EC知∠1=∠3、由OD=OB知∠2=∠4,根据BC是⊙O的切线得∠3+∠4=90°,即∠1+∠2=90°,得证;
(2)由sin∠F=$\frac{BE}{EF}$=$\frac{1}{2}$知∠F=30°,在Rt△ODF中,根据OD=DFtan∠F可得答案.
解答 解:(1)如图,连接OD,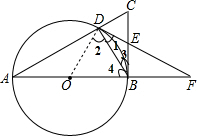 ∵AB为⊙O的直径,
∵AB为⊙O的直径,
∴∠ADB=∠BDC=90°,
在Rt△BDC中,∵BE=EC,
∴DE=EC=BE,
∴∠1=∠3,
∵BC是⊙O的切线,
∴∠3+∠4=90°,
∴∠1+∠4=90°,
又∵∠2=∠4,
∴∠1+∠2=90°,
∴DF为⊙O的切线;
(2)∵EF=2DE=4,
∴DE=BE=2,
在Rt△BEF中,∵sin∠F=$\frac{BE}{EF}$=$\frac{2}{4}$=$\frac{1}{2}$,
∴∠F=30°,
∴在Rt△ODF中,OD=DFtan∠F=6×$\frac{\sqrt{3}}{3}$=2$\sqrt{3}$,
即⊙O的半径为2$\sqrt{3}$.
点评 本题主要考查切线的判定与性质及直角三角形的性质、圆周角定理及三角函数的应用,掌握圆周角定理和切线的性质和判定是解题的关键.

练习册系列答案
相关题目
11.“五四”青年节期间,某团委举办了“我的中国梦”演讲知识竞赛,并将成绩制成如图所示的扇形统计图和条形统计图,根据图中提供的信息,这些参加演讲的同学的中位数和平均数分别是( )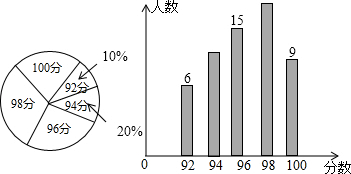

| A. | 94分,96分 | B. | 96分,96分 | C. | 94分,96.4分 | D. | 96分,96.4分 |
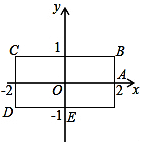 如图,长方形BCDE的各边分别平行于x轴或y轴,物体甲和物体乙分别由点A(2,0)同时出发,沿长方形BCDE的边作环绕运动.物体甲按逆时针方向以1个单位/秒匀速运动,物体乙按顺时针方向以2个单位/秒匀速运动,则两个物体运动后的第2017次相遇地点的坐标是(-1,1).
如图,长方形BCDE的各边分别平行于x轴或y轴,物体甲和物体乙分别由点A(2,0)同时出发,沿长方形BCDE的边作环绕运动.物体甲按逆时针方向以1个单位/秒匀速运动,物体乙按顺时针方向以2个单位/秒匀速运动,则两个物体运动后的第2017次相遇地点的坐标是(-1,1).