题目内容
19.下列哪个是最简二次根式( )| A. | $\sqrt{8}$ | B. | $\sqrt{12}$ | C. | $\sqrt{18}$ | D. | $\sqrt{5}$ |
分析 化简得到结果,即可做出判断.
解答 解:A、$\sqrt{8}$=2$\sqrt{2}$,此选项错误;
B、$\sqrt{12}$=2$\sqrt{3}$,此选项错误;
C、$\sqrt{18}$=3$\sqrt{2}$,此选项错误;
D、$\sqrt{5}$是最简二次根式,此选项正确;
故选D.
点评 此题考查了最简二次根式,熟练掌握二次根式的化简公式是解本题的关键.

练习册系列答案
相关题目
9. 如图,已知点D是AB边的中点,AF∥BC,CG:GA=3:1,BC=8,则AF等于( )
如图,已知点D是AB边的中点,AF∥BC,CG:GA=3:1,BC=8,则AF等于( )
 如图,已知点D是AB边的中点,AF∥BC,CG:GA=3:1,BC=8,则AF等于( )
如图,已知点D是AB边的中点,AF∥BC,CG:GA=3:1,BC=8,则AF等于( )| A. | 2 | B. | 4 | C. | 16 | D. | 8 |
10.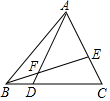 D、E分别为△ABC中BC、AC边上的点,且BD:DC=1:3,AE:EC=2:1,则AF:FD=( )
D、E分别为△ABC中BC、AC边上的点,且BD:DC=1:3,AE:EC=2:1,则AF:FD=( )
 D、E分别为△ABC中BC、AC边上的点,且BD:DC=1:3,AE:EC=2:1,则AF:FD=( )
D、E分别为△ABC中BC、AC边上的点,且BD:DC=1:3,AE:EC=2:1,则AF:FD=( )| A. | 3:1 | B. | 5:1 | C. | 8:1 | D. | 9:1 |
7.如果一个数的绝对值比它本身大,那么这个数为( )
| A. | 正数 | B. | 负数 | ||
| C. | 整数 | D. | 不等于零的有理数 |
14.下列命题中,真命题的个数是( )
①经过三点一定可以作圆;
②任意一个圆一定有一个内接三角形,并且只有一个内接三角形.
③任意一个三角形一定有一个外接圆,并且只有一个外接圆;
④三角形的内心到三角形的三个顶点距离相等.
①经过三点一定可以作圆;
②任意一个圆一定有一个内接三角形,并且只有一个内接三角形.
③任意一个三角形一定有一个外接圆,并且只有一个外接圆;
④三角形的内心到三角形的三个顶点距离相等.
| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
4.下列语句中,正确的有( )
①关于一条直线对称的两个图形一定能重合;
②两个能重合的图形一定关于某条直线对称;
③一个轴对称图形不一定只有一条对称轴;
④两个轴对称图形的对应点一定在对称轴的两侧.
⑤角平分线上任意一点到角的两边的线段长相等.
①关于一条直线对称的两个图形一定能重合;
②两个能重合的图形一定关于某条直线对称;
③一个轴对称图形不一定只有一条对称轴;
④两个轴对称图形的对应点一定在对称轴的两侧.
⑤角平分线上任意一点到角的两边的线段长相等.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
11.若一个数的绝对值的相反数是-$\frac{1}{7}$,则这个数是( )
| A. | -$\frac{1}{7}$ | B. | +$\frac{1}{7}$ | C. | ±$\frac{1}{7}$ | D. | ±7 |
8. 如图:△ABC≌△BAD,如果AB=5,BD=4,AD=6,那么BC的长是( )
如图:△ABC≌△BAD,如果AB=5,BD=4,AD=6,那么BC的长是( )
 如图:△ABC≌△BAD,如果AB=5,BD=4,AD=6,那么BC的长是( )
如图:△ABC≌△BAD,如果AB=5,BD=4,AD=6,那么BC的长是( )| A. | 6 | B. | 5 | C. | 4 | D. | 无法确定 |