题目内容
19.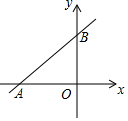 如图,直线AB分别交x轴,y轴于点A(-4,0),B(0,3),点C为y轴上的点,若以点C为圆心,CO长为半径的圆与直线AB相切时,则点C的坐标为(0,$\frac{4}{3}$)或(0,-12).
如图,直线AB分别交x轴,y轴于点A(-4,0),B(0,3),点C为y轴上的点,若以点C为圆心,CO长为半径的圆与直线AB相切时,则点C的坐标为(0,$\frac{4}{3}$)或(0,-12).
分析 设C(0,t),作CH⊥AB于H,如图,利用勾股定理计算出AB=5,利用切线的性质得CH=OC,讨论:当t>3时,BC=t-3,CH=t,证明△BHC∽△BOA,利用相似比可计算出t=-12,舍去;当0<t<3时,BC=3-t,CH=t,同样证明△BHC∽△BOA,利用相似比计算出t=$\frac{4}{3}$,当t<0时,BC=3-t,CH=-t,同样证明△BHC∽△BOA,利用相似比计算出t=-12,从而得到C点坐标.
解答 解:设C(0,t),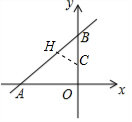 作CH⊥AB于H,如图,AB=$\sqrt{O{B}^{2}+O{A}^{2}}$=5,
作CH⊥AB于H,如图,AB=$\sqrt{O{B}^{2}+O{A}^{2}}$=5,
∵以点C为圆心,CO长为半径的圆与直线AB相切,
∴CH=OC,
当t>3时,BC=t-3,CH=t,
∵∠CBH=∠ABC,
∴△BHC∽△BOA,
∴CH:OA=BC:BA,即t:4=(t-3):5,解得t=-12(舍去)
当0<t<3时,BC=3-t,CH=t,同样证明△BHC∽△BOA,
∴CH:OA=BC:BA,即t:4=(3-t):5,解得t=$\frac{4}{3}$,
当t<0时,BC=3-t,CH=-t,同样证明△BHC∽△BOA,
∴CH:OA=BC:BA,即-t:4=(3-t):5,解得t=-12,
综上所述,C点坐标为(0,$\frac{4}{3}$)或(0,-12).
故答案为(0,$\frac{4}{3}$)或(0,-12).
点评 本题考查了切线的性质:圆的切线垂直于经过切点的半径;经过圆心且垂直于切线的直线必经过切点.也考查了坐标与图形性质和分类讨论思想的应用.

练习册系列答案
相关题目
9.抛物线C1:y1=a1x2+b1x+c1中,函数值y1与自变量x之间的部分对应关系如下表:
(1)设抛物线C1的顶点为P,则点P的坐标为(-1,0);
(2)现将抛物线C1沿x轴翻折,得到抛物线C2:y2=a2x2+b2x+c2,试求C2的解析式;
(3)现将抛物线C2向下平移,设抛物线在平移过程中,顶点为点D,与x轴的两交点为点A、B.
①在最初的状态下,至少向下平移多少个单位,点A、B之间的距离不小于6个单位?
②在最初的状态下,若向下平移m(m>0)个单位时,对应的线段AB长为n,请直接写出m与n的等量关系.
| x | … | -3 | -2 | -1 | 1 | 3 | 4 | … |
| y1 | … | -4 | -1 | 0 | -4 | -16 | -25 | … |
(2)现将抛物线C1沿x轴翻折,得到抛物线C2:y2=a2x2+b2x+c2,试求C2的解析式;
(3)现将抛物线C2向下平移,设抛物线在平移过程中,顶点为点D,与x轴的两交点为点A、B.
①在最初的状态下,至少向下平移多少个单位,点A、B之间的距离不小于6个单位?
②在最初的状态下,若向下平移m(m>0)个单位时,对应的线段AB长为n,请直接写出m与n的等量关系.
4.下列各数中,相反数为4的是( )
| A. | 4 | B. | -4 | C. | 0.4 | D. | 0.25 |
9.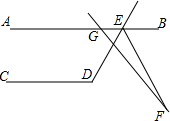 如图,AB∥CD,∠CDE=119°,GF交∠DEB的平分线EF于点F,∠AGF=130°,则∠F的度数是( )
如图,AB∥CD,∠CDE=119°,GF交∠DEB的平分线EF于点F,∠AGF=130°,则∠F的度数是( )
 如图,AB∥CD,∠CDE=119°,GF交∠DEB的平分线EF于点F,∠AGF=130°,则∠F的度数是( )
如图,AB∥CD,∠CDE=119°,GF交∠DEB的平分线EF于点F,∠AGF=130°,则∠F的度数是( )| A. | 10.5° | B. | 9.5° | C. | 8.5° | D. | 8° |
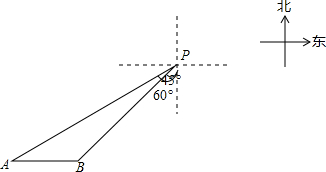 一艘轮船位于灯塔P南偏西60°方向,距离灯塔200海里的A处,它向东航行多少海里到达灯塔P南偏西45°方向上的B处(参考数据:$\sqrt{3}$≈1.732,结果精确到0.1)?
一艘轮船位于灯塔P南偏西60°方向,距离灯塔200海里的A处,它向东航行多少海里到达灯塔P南偏西45°方向上的B处(参考数据:$\sqrt{3}$≈1.732,结果精确到0.1)?
 如图,抛物线y=$\frac{\sqrt{3}}{3}$x2-$\frac{2\sqrt{3}}{3}$x+c与y轴交于点A(0,-$\sqrt{3}$),与x轴交于B、C两点,其对称轴与x轴交于点D,直线l∥AB且过点D.
如图,抛物线y=$\frac{\sqrt{3}}{3}$x2-$\frac{2\sqrt{3}}{3}$x+c与y轴交于点A(0,-$\sqrt{3}$),与x轴交于B、C两点,其对称轴与x轴交于点D,直线l∥AB且过点D.