题目内容
9.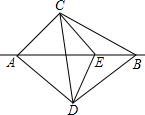 如图,AC=AD,∠CAB=∠DAB,E是直线AB上一个动点,连接EC,ED,问EC与ED,∠CEA与∠DEA之间有什么关系?就E点的不同位置加以证明.
如图,AC=AD,∠CAB=∠DAB,E是直线AB上一个动点,连接EC,ED,问EC与ED,∠CEA与∠DEA之间有什么关系?就E点的不同位置加以证明.
分析 根据SAS易证△ACE≌△ADE,所以EC=ED,∠CEA=∠DEA.
解答 解:EC=ED,∠CEA=∠DEA.
在△ACE和△ADE中,
$\left\{\begin{array}{l}{AC=AD}\\{∠CAB=∠DAB}\\{AE=AE}\end{array}\right.$,
∴△ACE≌△ADE,
∴EC=ED,∠CEA=∠DEA.
点评 本题考查了全等三角形的判定;本题是一道结论开放性题目,要找到图中的隐含条件,根据全等三角形的判定定理证明.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
20.2014年12月12日南水北调中线工程正式通水,每年可向北方输送95亿立方米的水量,95亿用科学记数法表示为( )
| A. | 9.5×107 | B. | 9.5×108 | C. | 9.5×109 | D. | 9.5×1010 |
17.已知关于x的一元二次方程(x+1)2=m有两个不等实数根,则m的取值范围是( )
| A. | m≥-1 | B. | m>0 | C. | m≥1 | D. | m≥0 |
18.今年由于降水明显偏少,气温持续偏高,河库水量锐减,据统计,某市造成直接经济损失达560 000 000元,该数据用科学记数法表示为( )
| A. | 5.6×107元 | B. | 5.6×108元 | C. | 56×107元 | D. | 56×108元 |
 如图,AB与CD相交于点O,若∠COB:∠BOD=5:1,则∠AOD=150°,∠AOC=30°.
如图,AB与CD相交于点O,若∠COB:∠BOD=5:1,则∠AOD=150°,∠AOC=30°.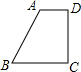 将如图所示的直角梯形绕直角边CD旋转一周,所得几何体的主视图是( )
将如图所示的直角梯形绕直角边CD旋转一周,所得几何体的主视图是( )


 观察如图,其中线段有3条,射线有8条.
观察如图,其中线段有3条,射线有8条. 如图,数轴上的点A,B表示的数分别是a-b,a+b.
如图,数轴上的点A,B表示的数分别是a-b,a+b.